The figure shows a snap photograph of a vibrating string at t = 0. The particle P is observed moving up with velocity 20√3 cm/s. The tangent at P makes an angle 60∘ with x-axis.
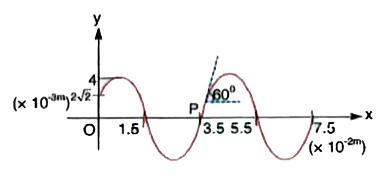
Find the total energy carried by the wave per cycle of the string. Assume that the mass per unit length of the string = 50 g/m.
1.6×10−5J
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - I)60videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)10videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)20videos
WAVE OPTICS
Similar Questions
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.
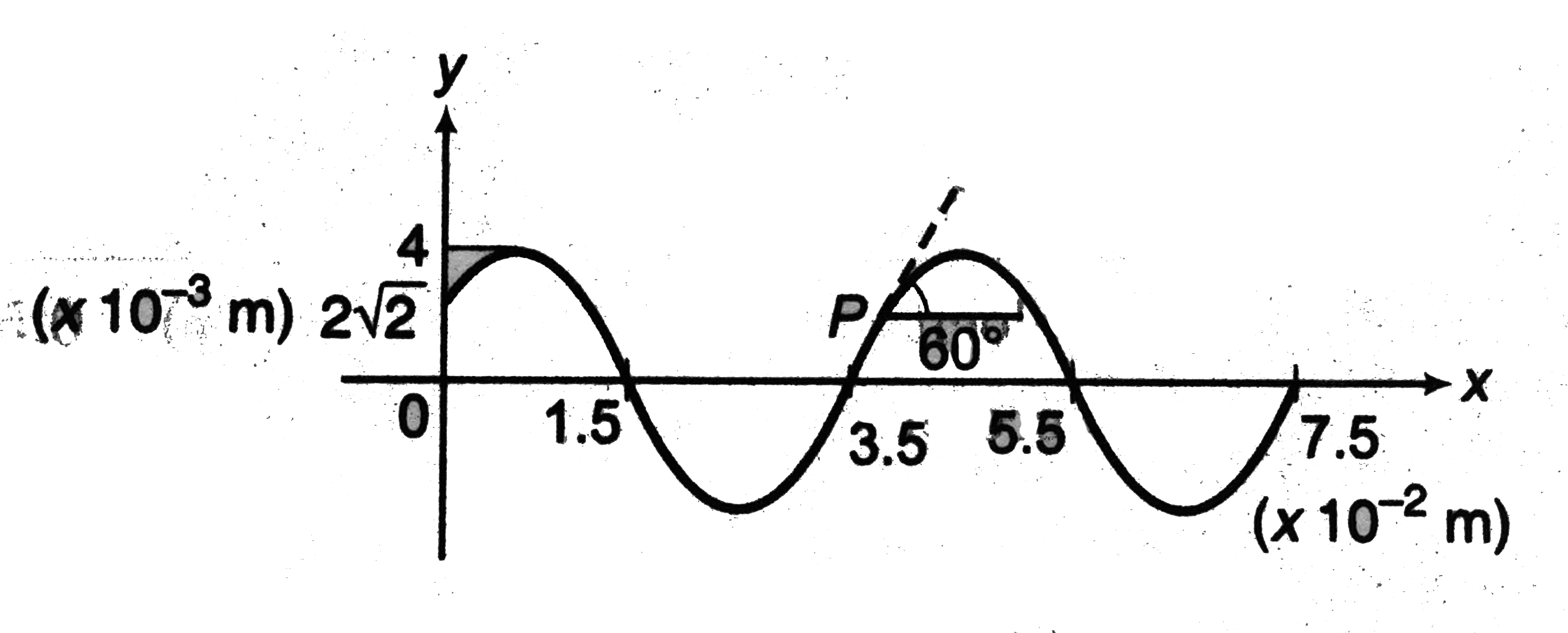
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.View SolutionThe figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.

(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.View Solution
Knowledge Check
- Question 1 - Select One
Three consecutive flash photographs of a travelling wave on a string wave on a string are reproduced in the figure here. The following oberservation are made. Mark the one which is correct. (Mass per unit length of the sting =3g/cm.)
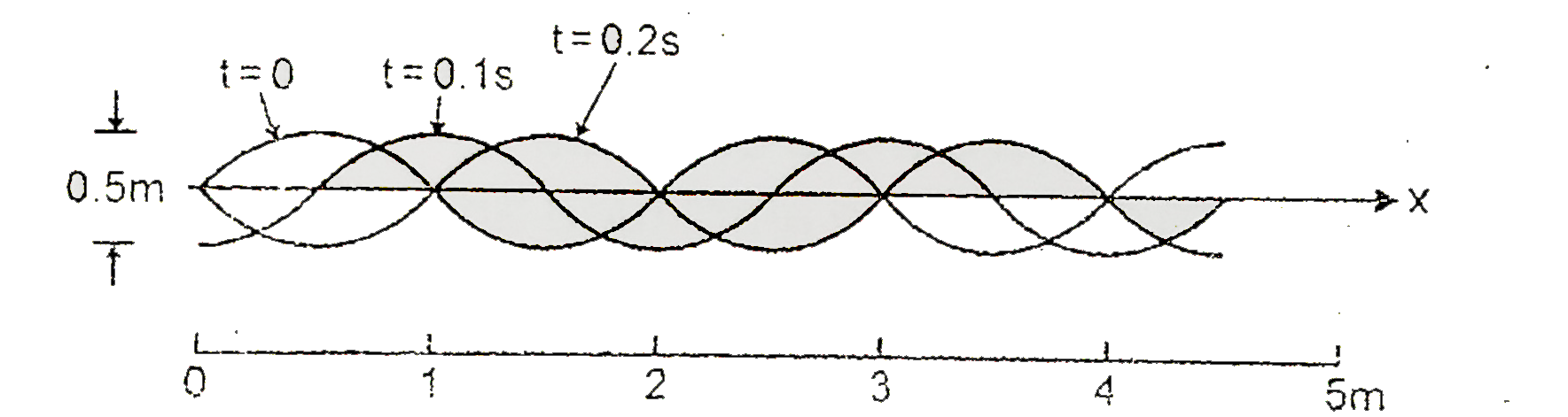 Adisplacement amplitude of the wave is 0.25m, wavelength is 1m, wave speed is 2.5m/s and the frequency of the driving force is 0.2/s.Bdisplacement amplitude of the wave is 2.0m, wavelength is 2m, wave speed is 0.4m/s and the frequency of the driving force is 0.7/s.Cdisplacement amplitude of the wave is 0.25m, wavelength is 2m, wave speed is 5m/s and the frequency of the driving force is 2.5/s.Ddisplacement amplitude of the wave is 0.5m, wavelength is 2m, wave speed is 2.5m/s and the frequency of the driving force is 0.2/s.
Adisplacement amplitude of the wave is 0.25m, wavelength is 1m, wave speed is 2.5m/s and the frequency of the driving force is 0.2/s.Bdisplacement amplitude of the wave is 2.0m, wavelength is 2m, wave speed is 0.4m/s and the frequency of the driving force is 0.7/s.Cdisplacement amplitude of the wave is 0.25m, wavelength is 2m, wave speed is 5m/s and the frequency of the driving force is 2.5/s.Ddisplacement amplitude of the wave is 0.5m, wavelength is 2m, wave speed is 2.5m/s and the frequency of the driving force is 0.2/s.
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.

(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.View SolutionA kite is flying at a height of 50√3 m from the horizontal. It is attached with a string and makes an angle 60∘ with the horizontal. Find the length of the string.
View SolutionA uniform string is clamped at x=0 and x = L and is vibrating in its fundamental mode. Mass per unit length of the string is μ, tension in it is T and the maximum displacement of its midpoint is A. Find the total energy stored in the string. Assume to be small so that changes in tension and length of the string can be ignored
View SolutionA uniform string is clamped at x=0 and x = L and is vibrating in its fundamental mode. Mass per unit length of the string is μ, tension in it is T and the maximum displacement of its midpoint is A. Find the total energy stored in the string. Assume to be small so that changes in tension and length of the string can be ignored
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
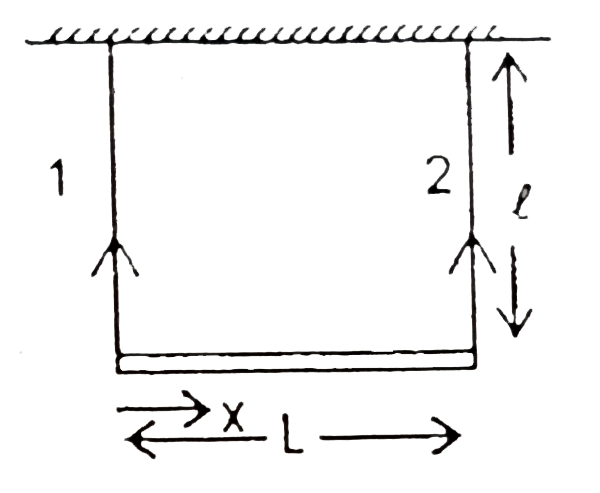 View Solution
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
 View Solution
View SolutionThree consecutive flash photographs of a travelling wave on a string wave on a string are reproduced in the figure here. The following oberservation are made. Mark the one which is correct. (Mass per unit length of the sting =3g/cm.)
 View Solution
View Solution

