Given that ¯x is the mean and σ2 is the variance of n observation x1,x2,…xn. Prove that the mean and σ2 is the variance of n observations ax1,ax2,ax3,….axn are a¯x and a2σ2, respectively, (a≠0).Solution in Gujrati
The correct Answer is:a2σ2
Step by step video, text & image solution for Given that bar(x) is the mean and sigma^(2) is the variance of n observation x_(1), x_(2), …x_(n). Prove that the mean and sigma^(2) is the variance of n observations ax_(1),ax_(2), ax_(3),….ax_(n) are abar(x) and a^(2)sigma^(2), respectively, (ane0). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - PRACTICE WORK
35 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - TEXTBOOK BASED MCQS
19 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - EXERCISE 5.3
5 Videos
- SETSBOOK - KUMAR PRAKASHANCHAPTER - SETSEXERCISE - QUESTION OF MODULE
28 Videos
- STRAIGHT LINESBOOK - KUMAR PRAKASHANCHAPTER - STRAIGHT LINESEXERCISE - Question of Module (Knowledge Test :)
18 Videos
Similar Questions
Find the mean deviation about the mean for the given data:
18,20,28,17,22,25,29,32,34
View SolutionThe sum of 20 observations of the deviation from 30 is 20. Their mean is
View SolutionFrom the data given below state which group is more variable, A or B?
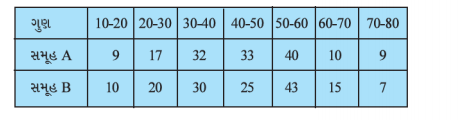
View SolutionA{x∈R∣x2+3=0} is a set of………type.
View SolutionFind distance between the points A(3,4)andB(−4,3).
View SolutionIf the mean of n observation ax1,ax2,ax3,,axn is a¯¯¯X , show that (ax1−a¯¯¯X)+(ax2−a¯¯¯X)++(axn−a¯¯¯X)=0
View SolutionLet x1, x2,...., xn values of variable X and let 'a' be non zero real number. Then prove that the variance of the observations ax1, ax2,..., axn is a2 Var (X) . Also, find their standard deviation.
View SolutionIf the arithmetic mean of the numbers x_(1),x_(2),x_(3),...,x_(n) is bar(x), then the arithmetic mean of the numbers ax_(1)+b,ax_(2)+b,ax_(3)+b,...,ax_(n)+b where a,b are two constants,would be
View SolutionGiven that ¯x is the mean and σ2 is the variance of n observations x1,x2,………….xn. Prove that the mean and variance of the observations ax1,ax2,ax3,………….axn are a¯x and a2σ2 , respectively, (a≠0)
View SolutionIf the mean and variance of the observations x1,x2,x3,…,xn are ¯xandσ2 respectively and a be a nonzero real number, then show that the mean and variance of ax1,ax2,ax3,…,axn are a¯xanda2σ2 respectively.
View Solutionयदि n प्रेक्षण x1,x2…xn का माध्ये ¯x तथा प्रेक्षण σ2 है तो सिद्ध कीजिये की प्रेक्षणों ax1,ax2,ax3…..axn का मध्य और प्रेक्षण क्रमशः a¯x तथा a2σ2(a≠0) है
View Solutionयदि n प्रेक्षणों ax1,ax2,ax3…,axn का माध्य a¯¯¯X है, तो सिद्ध कीजिए कि (ax1−a¯¯¯X)+(ax2−a¯¯¯X)+…+(axn−a¯¯¯X)=0
View SolutionIf the values of variable X are x1,x2,.......xn, then the variance of ax1,ax2,.......axn (a is any non-zero real number) is
View SolutionGiven that ¯x is the mean and σ2 is the variance of n observation x1,x2,…xn. Prove that the mean and σ2 is the variance of n observations ax1,ax2,ax3,….axn are a¯x and a2σ2, respectively, (a≠0).
View SolutionGiven that ¯x is the mean and σ2 is the variance of n observation x1,x2,…xn. Prove that the mean and σ2 is the variance of n observations ax1,ax2,ax3,….axn are a¯x and a2σ2, respectively, (a≠0).
View SolutionGiven that ¯x is the mean and σ2 is the variance of n observation x1,x2,…xn. Prove that the mean and σ2 is the variance of n observations ax1,ax2,ax3,….axn are a¯x and a2σ2, respectively, (a≠0).
View Solution
