कथन-I : समान्तर चतुभुज जिसकी भुजाये lx+my+n=0,lx+my+n'=0,mx+ly+n=0,mx+ly+n'=0 हो, के विकर्ण लम्बवत् होंगे। क्योंकि
कथन-II : यदि समान्तर चतुर्भुज की समान्तर भुजाओं के मध्य लम्बवत् दूरी समान हो, तो यह समचतुर्भुज होगा।
कथन-I सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है : कथन-II, कथन-I का सही स्पष्टीकरण नहीं है|
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन- असत्य है परन्तु कथन-II सत्य है।
The correct Answer is:A
Step by step video, text & image solution for कथन-I : समान्तर चतुभुज जिसकी भुजाये lx + my + n = 0, lx + my + n' = 0, mx + ly + n = 0, mx + ly + n'=0 हो, के विकर्ण लम्बवत् होंगे। क्योंकि कथन-II : यदि समान्तर चतुर्भुज की समान्तर भुजाओं के मध्य लम्बवत् दूरी समान हो, तो यह समचतुर्भुज होगा। by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) (गद्यांश # 1:)3videos
बिन्द् एवं सरल रेखा
- BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) (गद्यांश # 2:)3videos
बिन्द् एवं सरल रेखा
- BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन (Match the column)2videos
बिन्द् एवं सरल रेखा
- BOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -04 [B]10videos
द्विपद प्रमेय
- BOOK - ALLEN HINDICHAPTER - लघुगणक EXERCISE - DO YOURSELF -62videos
लघुगणक
Similar Questions
एक गतिमान बिन्दु का बिन्दुपथ वह पथ है, जो वह बिन्दु दिये गए एक या अधिक ज्यामितिय प्रतिबंधों में, मम्करता हुआ बनाता है। बिन्दु का बिन्दुपथ ज्ञात करने के लिए बिन्दु के निर्देशांक (h, k) मानते है, तथा प्रश्न में दिये गये प्रतिबन्धों प्लेतथाk के मध्य सम्बन्ध ज्ञात करने का प्रयास करते है। यदि इस विधि में कोई भी चर होता है तो हम उसे विलुप्त करते है। अन्त में ईको x से तथाk को 7 से पुनः स्थापित करके ज्ञात करते है जो कि बिन्दु का अभीष्ठ बिन्दुपथ है, जो कि वy में समीकरण होगी।
त्रिभुज जिसके शीर्ष (acost, asint), (bsint, – bcost) तथा (1,0) है, जहाँ t एक प्राचल है, के केन्द्रक का बिन्दुपथ है|05:18View Solutionनिर्देशी तल के बिन्दुओं P≡(x1,y1) तथा Q≡(x2,y2) के लिए, नई दूरी d(P, Q) निम्न सूत्र द्वारा परिभाषित होती है। d(P,Q)=|x1−x2|+|y1−y2|
माना O≡(0,0),A≡(1,2),B≡(2,3) तथा C≡(4,3),x−y तल में चार स्थिर बिन्दु है।
माना R(x, y) इस प्रकार है कि नई दूरी के अनुसार R बिन्दुओं o तथा A से समान दूरी पर है तथा यदि 0≤x<1 व 0≤y<2 तब R एक रेखाखण्ड पर स्थित होगा जिसकी समीकरण है-02:58View Solutionनिम्न प्रश्नों में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमे (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकिस्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा नामित किया गया है।स्तम्भ-I(Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Columm-II) के एक वक्तव्य से सही सुमेल करता है।
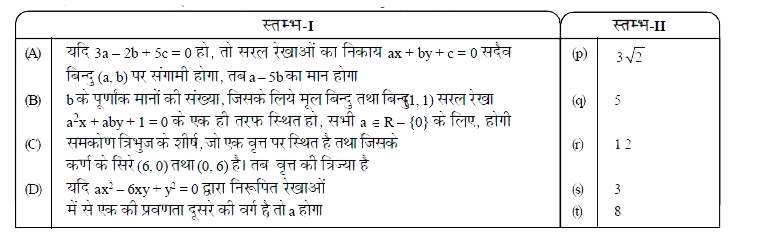 06:45View Solution
06:45View Solutionयदि 2n∑r=0ar(x−2)r=2n∑r=0br(x−3)r और सभी k≥n के लिए ak=1 तो दिखाइए की bn=2n+1Cn+1
04:40View Solutionहल कीजिए :|x+3|=2(5−x)
05:58View SolutionThe diagonals of the parallelogram whose sides are lx+my+n=0lx+my+n',=0,mx+ly+n=0mx+ly+n'=0 include an angle
03:04View SolutionThe lines lx+my+n=0,mx+ny+l=0 and nx+ly+m=0 are concurrent if (where l!=m!=n)
05:58View SolutionThe lines (lx+my)2−3(mx−ly)2=0 and lx+my+n=0 forms
03:37View Solutionएक समांतर चतुर्भुज की भुजाएं
lx+my+n=0,
lx+my+n’=0
mx+ly+n=0 तथा mx+ly+n’=0 है तो इनके विकर्णों के बीच का कोण होगा05:14View SolutionThe diagonals of the parallelogram whose sides are lx+my+n=0,lx+my+n1=0,mx+ly+n=0,mx+ly=n1=0 include an angle
02:43View Solutionएक समान्तर चतुर्भुज की भुजायें x + my+n = 0, ix+my+n'=0,mx+ly+n=0,mx+ly+n'=0 हैं, तो इनके विकर्णों के बीच कोण होगा
05:57View SolutionThe diagonals of the parallelogram whose sides are lx+my+n=0,lx+my+n1=0,mx+ly+n=0,mx+ly=n1=0 include an angle
10:52View SolutionThe straight lines joining the origin to the points of intersection of the line 2x+y=1 and curve 3x2+4xy−4x+1=0 include an angle
07:56View SolutionShow that the lines lx + my + n = 0 , mx + ny + l = 0 and nx + ly + m = 0 are concurrent, if l + m + n = 0.
06:43View SolutionShow that the lines lx+my+n=0,mx+ny+l=0andnx+ly+m=0 are concurrent if l+m+n=0
07:02View Solution

