निर्देशी तल के बिन्दुओं P≡(x1,y1) तथा Q≡(x2,y2) के लिए, नई दूरी d(P, Q) निम्न सूत्र द्वारा परिभाषित होती है। d(P,Q)=|x1−x2|+|y1−y2|
माना O≡(0,0),A≡(1,2),B≡(2,3) तथा C≡(4,3),x−y तल में चार स्थिर बिन्दु है।
माना T(x.y) इस प्रकार है कि नई दूरी के अनुसार T, बिन्दुओं O तथा C से समान दूरी पर है तथा यदि प्रथम चतुर्थांश में स्थित है, तब निश्चित लम्बाई की रेखा खण्ड तथा अनन्त किरणो का संयोजन है, जिसका चिम्ति चित्र है-
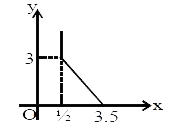

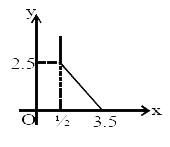
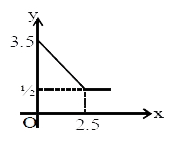
The correct Answer is:A
Step by step video, text & image solution for निर्देशी तल के बिन्दुओं P-= (x_(1),y_(1)) तथा Q-= (x_(2),y_(2)) के लिए, नई दूरी d(P, Q) निम्न सूत्र द्वारा परिभाषित होती है। d(P, Q) = |x_1 - x_2| + |y_1 - y_2| माना O -= (0, 0), A -= (1, 2), B -= (2, 3) तथा C -= (4, 3), x - y तल में चार स्थिर बिन्दु है। माना T(x.y) इस प्रकार है कि नई दूरी के अनुसार T, बिन्दुओं O तथा C से समान दूरी पर है तथा यदि प्रथम चतुर्थांश में स्थित है, तब निश्चित लम्बाई की रेखा खण्ड तथा अनन्त किरणो का संयोजन है, जिसका चिम्ति चित्र है- by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE)
19 Videos
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)
14 Videos
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) (गद्यांश # 1:)
3 Videos
- द्विपद प्रमेयBOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -04 [B]
10 Videos
- लघुगणक BOOK - ALLEN HINDICHAPTER - लघुगणक EXERCISE - DO YOURSELF -6
2 Videos
Similar Questions
बिन्दु P(3, 5), A(1,3) तथा B(7,9) मिलाने वाली रेखा को किस अनुपात में विभाजित करेगा। A तथा B के सापेक्ष P का हरात्मक संयुग्मी ज्ञात कीजिए।
View Solution(-2,-7) से गुजरने वाली तथा सरल रेखाओं 4x + 3y = 12 एवं 4x +3y=3 के मध्य 3 इकाई का अन्तः खण्ड काटने वाली रेखाओं की समीकरण ज्ञात कीजिए।
View Solutionएक गतिमान बिन्दु का बिन्दुपथ वह पथ है, जो वह बिन्दु दिये गए एक या अधिक ज्यामितिय प्रतिबंधों में, मम्करता हुआ बनाता है। बिन्दु का बिन्दुपथ ज्ञात करने के लिए बिन्दु के निर्देशांक (h, k) मानते है, तथा प्रश्न में दिये गये प्रतिबन्धों प्लेतथाk के मध्य सम्बन्ध ज्ञात करने का प्रयास करते है। यदि इस विधि में कोई भी चर होता है तो हम उसे विलुप्त करते है। अन्त में ईको x से तथाk को 7 से पुनः स्थापित करके ज्ञात करते है जो कि बिन्दु का अभीष्ठ बिन्दुपथ है, जो कि वy में समीकरण होगी।
त्रिभुज जिसके शीर्ष (acost, asint), (bsint, – bcost) तथा (1,0) है, जहाँ t एक प्राचल है, के केन्द्रक का बिन्दुपथ है|
View Solutionयदि 2n∑r=0ar(x−2)r=2n∑r=0br(x−3)r और सभी k≥n के लिए ak=1 तो दिखाइए की bn=2n+1Cn+1
View Solutionहल कीजिए :|x+3|=2(5−x)
View SolutionIf the circle x^(2)+y^(2)=a^(2) intersects the hyperbola xy=c^(2) in four points P(x_(1),y_(1))Q(x_(2),y_(2)),R(x_(3),y_(3)),S(x_(4),y_(4)), then which of the following need not hold. (a) x_(1)+x_(2)+x_(3)+x_(4)=0 (b) x_(1)x_(2)x_(3)x_(4)=y_(1)y_(2)y_(3)y_(4)=c^(4) (c) y_(1)+y_(2)+y_(3)+y_(4)=0 (d) x_(1)+y_(2)+x_(3)+y_(4)=0
View SolutionIf the circle x^(2)+y^(2)=a^(2) intersects the hyperbola xy=c^(2) in four points P(x_(1),y_(1))Q(x_(2),y_(2)),R(x_(3),y_(3)),S(x_(4),y_(4)), then which of the following need not hold. (a) x_(1)+x_(2)+x_(3)+x_(4)=0 (b) x_(1)x_(2)x_(3)x_(4)=y_(1)y_(2)y_(3)y_(4)=c^(4) (c) y_(1)+y_(2)+y_(3)+y_(4)=0 (d) x_(1)+y_(2)+x_(3)+y_(4)=0
View SolutionIf the circle x^(2)+y^(2)=a^(2) intersects the hyperbola xy=c^(2) in four points P(x_(1),y_(1))Q(x_(2),y_(2)),R(x_(3),y_(3)),S(x_(4),y_(4)), then which of the following need not hold. (a) x_(1)+x_(2)+x_(3)+x_(4)=0 (b) x_(1)x_(2)x_(3)x_(4)=y_(1)y_(2)y_(3)y_(4)=c^(4) (c) y_(1)+y_(2)+y_(3)+y_(4)=0 (d) x_(1)+y_(2)+x_(3)+y_(4)=0
View SolutionIf the normal at the point P(x_(i),y_(i)),i=1,2,3,4 on the hyperbola xy=c^(2) are concurrent at the point Q(h,k) then _((x_(1)+x_(2)+x_(3)+x_(4))(y_(1)+y_(2)+y_(3)+y_(4)))((x_(1)+x_(2)+x_(3)+x_(4))(y_(1)+y_(2)+y_(3)+y_(4)))/(x_(1)x_(2)x_(3)x_(4)) is
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View SolutionIf the circle x2+y2=a2 intersects the hyperbola xy=c2 in four points P(x1,y1) Q(x2,y2) R(x3,y3) S(x4,y4) then 1) x1+x2+x3+x4=2c2 2) y1+y2+y3+y4=0 3) x1x2x3x4=2c4 4) y1y2y3y4=2c4
View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionवह अनुपात ज्ञात कीजिए जिसमें बिंदुओं P(x1,y1,z1) तथा Q(x2,y2,z2) को मिलाने वाली रेखा , समतल ax + by + cz + d = 0 व्दारा विभाजित होती है ।
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionदो रेखाएं x−31=y+13=z−6−1 तथा x+57=y−2−6=z−34 बिन्दु R पर काटती है । बिन्दु R के XY तल के प्रतिबिम्ब के निर्देशांक है
View Solution
