कथन I: यदि z=i+2i2+3i3+…………+32i32 हो तो z,¯z,−z व −¯z आर्गण्ड तल में वर्ग के शीर्ष है।
क्योंकि
कथन –II z,¯z,−z,−¯z आर्गण्ड तल पर मूल बिंदु से समान दूरी पर स्थित है।
कथन- सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है , कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन - I सत्य है परन्तु कथन - II असत्य है।
कथन - Iअसत्य है परन्तु कथन - II सत्य है।
The correct Answer is:B
Step by step video, text & image solution for कथन I: यदि z=i+2i^(2)+3i^(3)+…………+32i^(32) हो तो z,barz,-z व -barz आर्गण्ड तल में वर्ग के शीर्ष है। क्योंकि कथन –II z,barz,-z,-barz आर्गण्ड तल पर मूल बिंदु से समान दूरी पर स्थित है। by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सम्मिश्र संख्या (COMPLEX NUMBER)BOOK - ALLEN HINDICHAPTER - सम्मिश्र संख्या (COMPLEX NUMBER)EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 1 :
3 Videos
- सम्मिश्र संख्या (COMPLEX NUMBER)BOOK - ALLEN HINDICHAPTER - सम्मिश्र संख्या (COMPLEX NUMBER)EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 2:
3 Videos
- सम्मिश्र संख्या (COMPLEX NUMBER)BOOK - ALLEN HINDICHAPTER - सम्मिश्र संख्या (COMPLEX NUMBER)EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) स्तम्भ सुमेलन (Match the column)
2 Videos
- सम्बन्ध BOOK - ALLEN HINDICHAPTER - सम्बन्ध EXERCISE - EXERCISE-II
6 Videos
Similar Questions
माना z कोई एक सम्मिश्र संख्या है। zn−1 रूप के व्यंजक को गुण्नख्ण्डित करने के लिए, हम समीकरण zn=1 को लेंगें। इस समीकरण को डी-मॉयवर प्रमेय के प्रयोग से हल करेंगें। माना 1,α1,α2,……..αn−1 इस समीकरण के मूल कै तो zn−1=(z−1)(z−α1)(z−α2)………….(z−αn−1) होगा। व्यंजक zn−kn के गुणनखण्ड करने केलिए इस विधि को व्यापक किया जा सकता है।
उदाहरणः z7+1=6∏m=0(z−CiS(2mπ7+π7))
इसको पुनः निम्न से सरलीकृत किया जा सकता है।
z7+1=(z+1)(z2−2zcosπ7+1)(z2−2zcos3π7+1)(z2−2zcos5π7+1)………(i)
यह विभाजक गुणनखण्ड त्रिकोणमितीय सर्वसमिकाओं को सि8 करने में महत्वपूर्ण है। उदाहरण यदि समीकरण (i) में हम z=i रखे तो समीकरण (i) निम्न परिवर्तित होगी:
(1−i)=(i+1)(−2icosπ7)(−2icos3π7)(−2icos5π7)
अर्थात cosπ7cos3π7cos5π7=−18
यदि व्यंजक z5−32 को रेखीय व द्विघात गुणनखण्डों में वास्वतिक गुणांकों के साथ लिखा जा सकता हो जैसे (z5−32)=(z−2)(z2−pz+4)(z2−qz+4) जहां p>q हो तो p2−2q का मान होगा:
View Solutionदिए गए चित्र में |z|=r, त्रिभुज ABC का परिवृत है। D, E व F क्रमशः भुजाओं BC, CA तथा AB के मध्य बिन्दु हैं। AD आगे बढ़ाने पर वृत्त को L पर मिलाता है। यदि ∠CAD=0,AD=x,BD=y और त्रिभुज ABC का बिन्दु A से डाला गया शीर्षलम्ब, वृत्त |z|=r को M पर मिलाता है। यदि बिन्दुओं A,B तथा C के आगम क्रमशः za,zb तथा zc है-
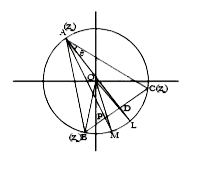
त्रिभुज ABC का क्षेत्रफल है -
View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I(Columm-I) के वक्तव्यों को A,B,C तथा नामित किया गया है जबकिस्तम्भ-II (Column-II) के वक्तव्यों क p.qr तथा s नामित किया गया है। स्तम्भ-I(Column-I) में दिए गएकोई एक वक्तव्यस्तम्भ-II (Column-II) के एक वक्तव्य से सही सुमेल करता है।

View Solutionमानाकि R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} समुच्चय A = {1, 2, 3, 4} में एक संबंध है, तब संबंध R होगा-
View SolutionIf |z|= maximum {|z+2|,|z−2|}, then(A)|z-¯z|=1/2(B)|z+¯z|=4(C)|z+¯z|= 1/2(D)|z−¯z=2
View SolutionIf |z+¯z|=|z−¯z|, then value of locus of z is
View SolutionIf |z+¯z|+|z−¯z|=2, then z lies on
View SolutionIf |z+¯z|+|z−¯z|=8, then z lies on
View Solutionif z=3 -2i, then verify that
(i) z+¯z=2Rez
(ii) z−¯z=2ilmz
View SolutionIf z=3+i , then (z+1)(¯z+1)=
View SolutionIf |z+¯z|+|z−¯z|=2 , then z lies on
View SolutionIf |Z-barZ|+|Z+barZ|=2 , Then the position of Z will be
View SolutionStatement - I : If z=¯z then z is purely imaginary
Statement- II : If z=−¯z then z is purely real
View SolutionIf |z+¯z|+|z−¯z|=2 then z lies on
View SolutionIf |z+¯z|+|z−¯z| , then the locus of z is
View SolutionIf z is a non zero complex, number then ∣∣ ∣∣|¯z|2z¯z∣∣ ∣∣ is equal to
(a). ∣∣∣¯zz∣∣∣
(b). |z|
(c). |¯z|
(d). none of these
View Solution
