माना निम्न दो समतल
P1≡[→r−→p,→a→b]=0
P2≡[→r−→p,→c.→d]=0
है, ताकि (→a×→b)×(→c×→d)=0 तथा माना समष्टि में कोई सदिश →x है।
कथन -1: →x.{(→a×→b)×(→c×→d)}=0⇒→x.{t1→a+t2→b}=0,∀t1,t2∈R
क्यूंकि कथन -II: →x.{t1→a+t2→b}=0∀t1,t2∈R⇒→x.{(→a×→b)×(→c×→d)}=0
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन-I असत्य है परन्तु कथन-II सत्य है।
The correct Answer is:D
Topper's Solved these Questions
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 1:
3 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 2:
3 Videos
- 3D-COORDINATE GEOMETRY BOOK - ALLEN HINDICHAPTER - 3D-COORDINATE GEOMETRY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) स्तम्भ सुमेलन (Match the column)
3 Videos
- PROBABILITYBOOK - ALLEN HINDICHAPTER - PROBABILITYEXERCISE - Exercise-05 [B] JEE-[Advanced] Previous Year Questions
34 Videos
Similar Questions
चार बिन्दु A(2, 1, 0), B(1, 0, 1), C(3, 0, 1) तथा D(0, 0, 2) दिए गए हैं। बिन्दु D, रेखा L पर स्थित है, जो बिन्दु A,B तथा C से बने समतल के लम्बकोणीय हैं। उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए :
समतल ABC का समीकरण है:
View Solutionयदि कोई रेखा P(x1,y1,z1) से गुजरती है तथा जिसके दिक् अनुपात a, b, c हों, तो रेखा का समीकरण x−x1a=y−y1b=z−z1c होगा तथा इसके लम्बवत् एवं P से गुजरने वाले समलत का समीकरण a(x−x1)+b(y−y1)+c(z−z1)=0 होगा और दो समतलों a1x+b1y+c1z+d1=0 तथा a2x+b2y+c2z+d2=0 के प्रतिच्छेद से गुजरने वाले समतल की समीकरण (a1x+b1y+c1z+d1)+k(a2x+b2y+c2z+d2)=0 होगी।
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए:
बिन्दु (1, -2, 3) की समतल x-y+z= 5 से, रेखा x2=y3=z−3−4 के समान्तर मापी गई दूरी होगी -
View Solutionनिम्न प्रश्नों में दो स्तम्भ में क्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है। स्तम्भ-I (Column-I) के वक्तव्यों कोA, B,C तथाD नामित किया गया है जबकिस्तम्भ-II (Column-II) के वक्तव्यों को, q, r तथा 5 नामित किया गया है। स्तम्भ-I(Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Columm-II) के एक वक्तव्य से सही सुमेल करता है।
निम्न समतल युग्म को उनकी प्रतिच्छेदी रेखाओं से सुमेलित कीजिए।
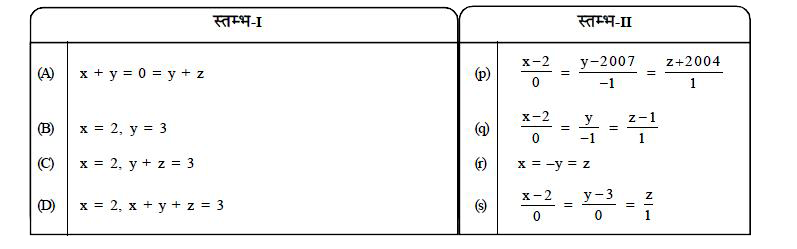
View Solutionयदि सिक्का 'n' बार उछाला जाता है , तो चित आने की प्रायिकता 'p' है। माना pn दो या अधिक बार लगातार चित नहीं आने की प्रायिकता है। सिद्ध कीजिए कि p1=1,p2=1−p2 तथा pn=(1−p)pn−1+p(1−p)pn−2 यदि n≥3 है।
View SolutionLet veca, vecb, vecc be three vectors such that a!=0 and veca xx vecb = 2veca xx vecc, |veca| = |vecc| = 1, |vecb| = 4 and |vecb xx vecc| = sqrt15. If vecb-2 vecc = lambda veca, then lambda is
View Solutionयदि (If) →X⋅→A=→X⋅→B=→X⋅→C=→0, जहाँ →X≠→0 तो सिद्ध करें कि [→A →B →C]=0.
View SolutionStatement-1: (→b+→c)।{(→c+→a)×(→a+→b)}=0।
Statement-2: यदि →p,→q और →r रैखिकीय आश्रित सदिश हो, तो वे समतलीय होंगे।
View SolutionLet →a=ˆi+2ˆj+3ˆk, →b=2ˆi+3ˆj+ˆk,→c=ˆk+ˆiand(→x×→b)=(→a×→c)×→b. If →x.→a=0 , then |→x| is equal to use √3=1.73)
View SolutionFor any four vectors →a,→b,→c,→d the expressions (→b×→c).(→a×→d)+(→c×→a).(→b×→d)+(→a×→b).(→c×→d)is always equal to:
View SolutionShow that (→a×→b)⋅(→c×→d)+(→b×→c)⋅(→a×→d)+(→c×→a)⋅(→b×→d)=0.
View Solutionयदि →x,→a,→b व →c अशून्य सदिश इस प्रकार हों, कि →a⋅→x=0,→b⋅→x=0 व →c⋅→x=0 हों, तब [→a→b→c] है
View Solution(→b×→c)⋅(→d×→a)−(→c×→d)⋅(→a×→b)−(→d×→a)⋅(→b×→c)−(→a×→b)⋅(→c×→d) बराबर है
View Solutionयदि →P=→b×→c[→a→b→c],→q=→c×→a[→a→b→c] तथा →r=→a×→b[→a×→b→c] जहाँ [→a→b→c]≠0 हो, तब →p⋅(→a+→b→c) का मान है
View SolutionIf →x.→a=0,→x.Vecb=0,→x.Ve=0 for some non-zero vector, →x, then [→a→b→c]=0 is :
View SolutionIf →a,→b,→cand→d are unit vectors such that (→a×→b).(→c×→d)=1and→a.Ve=12 then :
View Solution
