P is a point on the parabola y2=4axandPQ is its focal chord. If PT is tangent at P and QN is normal at Q, the angle α, between PTandQN , distance between PT and QN is 'd' then
a)0∘<α<90∘
b)α=0∘
c)d=0
d)a(1+t2)3/2t2
Step by step video & image solution for P is a point on the parabola y^2= 4ax and PQ is its focal chord. If PT is tangent at P and QN is normal at Q, the angle alpha, between PT and QN , distance between PT and QN is 'd' then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - A DAS GUPTACHAPTER - ParabolaEXERCISE - EXERCISE51videos
Parabola
- BOOK - A DAS GUPTACHAPTER - Pair of Straight Lines and Transformation of AxesEXERCISE - EXERCISE22videos
Pair of Straight Lines and Transformation of Axes
- BOOK - A DAS GUPTACHAPTER - Product of three or more VectorsEXERCISE - Exercise28videos
Product of three or more Vectors
Similar Questions
(0)2√1+1212 (C) 3 P is a point ‘t' on the parabola y2= 4ax and PQis a focal chord. PT is a tangent at P and QN is a normal at Q. The minimum distance between PT and QN is equal to 150 (B) a V1+t + (A) 0 1+ t2 a(t2 2
View SolutionIn Figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If angle POQ = 70°, then angleTPQ is equal to
View Solution
Knowledge Check
- Question 1 - Select One
In the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =
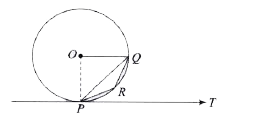 A100∘B110∘C120∘D150∘
A100∘B110∘C120∘D150∘ - Question 2 - Select One
P is a point on the parabola y2=4ax whose ordinate is equal to its abscissa and PQ is focal chord, R and S are the feet of the perpendiculars from P and Q respectively on the tangent at the vertex, T is the foot of the perpendicular from Q to PR, area of the triangle PTQ is
A75a2/4B85a2/2C75a2/8D45a2/2 - Question 3 - Select One
The distance between a tangent to the parabola y2=4ax which is inclined to axis at an angle α to X axis. and a parallel normal is
Aacosαsin2αBasinαcos2αCasinαcos2αDacosαsin2α
If the normals to the parabola y2=4ax at P meets the curve again at Q and if PQ and the normal at Q make angle α andβ , respectively, with the x-axis, then tanα(tanα+tanβ) has the value equal to 0 (b) −2 (c) −12 (d) −1
View SolutionIf PQ is the focal chord of the parabola y2=−xandP is (−4,2), then the ordinate of the point of intersection of the tangents at P and Q is
View SolutionIf the angle between the normal to the parabola y2=4ax at point P and the focal chord passing through P is 60∘, then find the slope of the tangent at point P.
View SolutionLet PQ be a focal chord of the parabola y2=4ax such that tangents at P and Q meet at point on the line y=2x+a,a>0, If PQ subtends an angle θ at the vertex of y2=4ax, then tan θ=
View SolutionLet the tangents at point P and R on the parabola y=x2 intersects at T. Tangent at point Q (lies in between the points P and R) on the parabola intersect PT and RT at A and B respectively. The value of TATP+TBTR is
View Solution

