Two bulbs of 100 c.c and 200 c.c capacity, contain the same gas at same temperature and pressure are connected by a capillary tube of negligible volume. Initially both were at C. Now the te,nperature of the bigger bulb is raised to C and that of the smaller bulb being kept at C. If the initial pressure was 76 cm of mercury, what is the final pressure?
Let P be the initial pressure of the bulbs and be the final pressure. Initial temperature of the bulbs be T. The final temperatures of the bulbs of volume be respectively.
By ideal gas equation, as mass of the gas in the bulbs remains constant
cm
Similar Questions
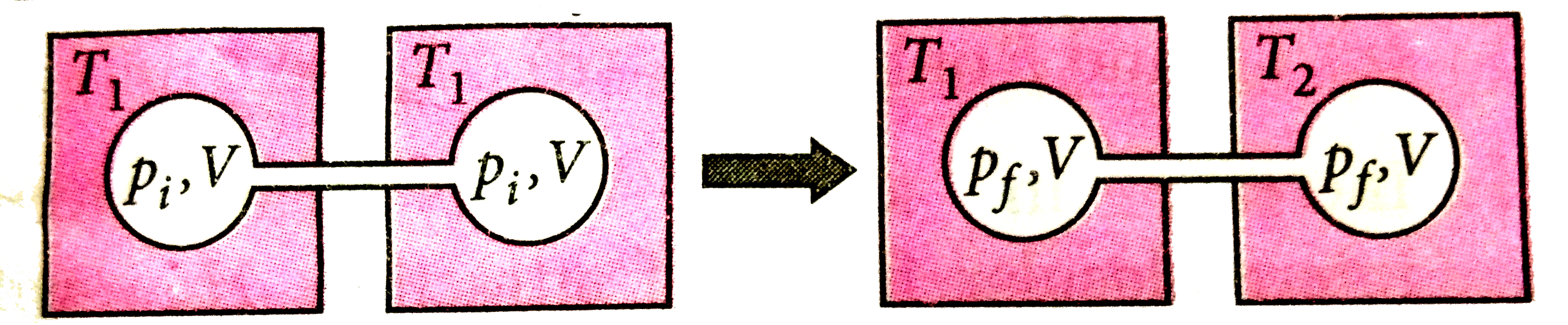
Two closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
 View Solution
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure pf is:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A one litre spherer and a two litre sphere are connected with a capillary tube of nefligible volume. They contain an idel gas at 270C at a pressure of 100cm of Hg. Keeping the temperature of one litre sphere constant at 270C, if temperature of two litre sphere is increased to 1270C, then the final pressure is
A110cm of HgB120cm of HgC150cm of HgD200cm of Hg - Question 2 - Select One
Two closed bulbs of equal volume (V) containing an ideal gas initially at pressure pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure pf is:
 A2p,(T2T1+T2)B2p,(T1T2T1+T2)Cp,(T1T2T1+T2)D2p,(T1T1+T2)
A2p,(T2T1+T2)B2p,(T1T2T1+T2)Cp,(T1T2T1+T2)D2p,(T1T1+T2) - Question 3 - Select One
Two closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure Pf is :
 Api(T1T2T1+T2)B2pi(T1T1+T2)C2Pi(T2T1+T2)D2pi(T1T2T1+T2)
Api(T1T2T1+T2)B2pi(T1T1+T2)C2Pi(T2T1+T2)D2pi(T1T2T1+T2)
400cc volume of gas having γ=52 is suddenly compressed to 100cc. If the initial pressure is P, the final pressure will be
View SolutionAir contained in a cylinder at 20.0∘C is compressed froma n initial pressure of 1.00 atm, and volume of 700cm3 to a volume of 70.0cm3 . If the final pressure is 15.0 atm then what is the final temperature?
View SolutionA glass bulb of volume 400cm3 is connected to another bulb of volume 200cm3 by means of a tube of negligible volume. The bulbs contain dry air and are both at a common temperature and pressure of 20∘C and 1.000 atm, respectively. The larger bulb is immersed in steam at 100∘C and the smaller in melting ice at 0∘. Find the final common pressure.
View Solution400cc volume of gas having γ=52 is suddenly compressed to 100cc. If the initial pressure is P, the final pressure will be
View SolutionTwo glass bulbs A (of 100 mL capacity), and B (of 150mL capacity) containing same gas are connected by a small tube of negligible volume. At particular temperature the pressure to A was found to be 20 times more than that in bulb B. the stopcock is opened without changing the temperature. the pressure in A will:
View Solution

