Two cells A and B with same e.m.f. of 2 V each and with internal resistance and are connected in series with an external resistance R = Find the terminal voltages across the two cells.
We know
Current through the circuit
i)
Terminal voltage across
volt
ii)
Terminal voltage across B,
volts
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
1 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - III
73 Videos
Similar Questions
Two cells A and B with same e.m.f of 2 V each and with internal resistances rA=3.5Ω and rB=0.5Ω are connected in series with an external resistance R=3Ω Find the terminal voltages across the two cells.
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
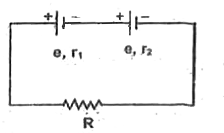
View Solution
Knowledge Check
Two cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris
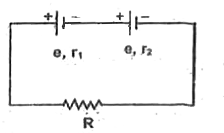 Ar1−r2Br1r2Cr1r2Dr1+r2
Ar1−r2Br1r2Cr1r2Dr1+r2Two cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
Ar1+r2Br1−r2Cr2−r1Dr21/r2Two cells of emf 3V and 5V and internal resistance r1 and r2 respectively are in series with an external resistance R. if the p.d. across 1 st cell is zero, then R is
A5r1−3r23B2r1−3r24C3r1−5r23D4r1−5r23
Two cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View Solution[" 27.Two cells of same emf "E" but of different internal resistance "r_(1)&r_(2)" are connected "],[" in series with an external resistance "R" .The potential drop across the first cell is "],[" found to be zero.The external resistance "R" is "]
View SolutionTwo identical cells of emf 1.5V and internal resistance 1Ω are joined in series and the combination is connected in parallel with a third cell of the same emf and internal resistance. Calculalte the terminal voltage of the cells.
View SolutionThe potential difference across terminals of cell of 20 V and r=2Ω connected to 8Ω external resistance is
View Solution
