The bob of simple pendulum having length 1, is displaced from mean position to an angular position o with respect to vertical. If it is released, then velocity of bob at equilibrium position is
√2g(1−cosθ)
√2g(1+cosθ)
√2glcosθ
√2gl
The correct Answer is:A
In △OAC,cosθ=OA/l or, OA=lcosθ
∴AB=1(1−cosθ)=h
At point C, the velocity of bob =0.
The vertical acceleration =g
∴v2=2gh or, v=√2gl(1−cosθ)
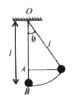
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:MTG-WBJEEChapter:OSCILLATIONS AND WAVESExercise:WB JEE WORKOUT (CATEGORY 2: SINGLE OPTION CORRECT TYPE 2 MARKS)
Explore 15 Videos
- OSCILLATIONS AND WAVESBook:MTG-WBJEEChapter:OSCILLATIONS AND WAVESExercise:WB JEE WORKOUT (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
Explore 10 Videos
- NUCLEAR PHYSICBook:MTG-WBJEEChapter:NUCLEAR PHYSICExercise:WB JEE PREVIOUS YEARS QUESTIONS
Explore 5 Videos
- PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMBook:MTG-WBJEEChapter:PARTICLE NATURE OF LIGHT AND WAVE PARTICLE DUALISMExercise:WB JEE PREVIOUS YEARS QUESTIONS
Explore 15 Videos
Similar Questions
The bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View SolutionThe bob of pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. Find the speed v with which the bob passes through the equilibrium position.
View Solution
Knowledge Check
A simple pendulum of bob mass m and length l is displaced from its mean position O to a point A and then released . If v is the velocity of the bob at O, h is the height of string of pendulum when bob passes through point O is /are (neglect friction )
A2mghlB2mg1+(h)lCmg1+(2h)lDmg1−(2h)lThe bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθThe bob of a pendulum of length l is pulled a side from its equilibrium position through an angle θ and then released the bob will then pass through its equilibrium position with a speed v where v equals to
A√2g1−sinθB√2g1+cosθC√2g1−cosθD√2g1+sinθ
The figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
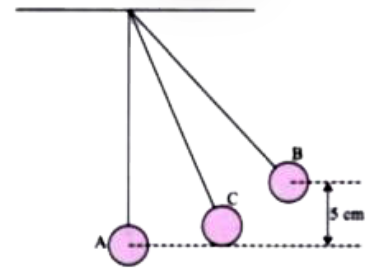
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
View SolutionThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be its lowest position ?
View SolutionThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be at its lowest position?
View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
View Solution
