Show that the charges oscillate with a frequency given by ω=1√LCwhen a charged capacitor of capacitance C is connected to an inductor of inductance L.
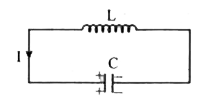
Consider a capacitor of capacitance C. Let it be charged q0 and connected to an ideal inductor of inductance L as shown in fig.
The capacitor begins to discharge. As it does so an emf is induced in the inductor. At any instant p.d. across the capacitor = p.d. across the inductor.
qC=−LdIdt
qC+ldldt=0
Where, q and I are the charge and current at any instant
But I=dIdt→(2)
∴qC+L(ddt)(dqdt)=0
(d2qdt2)+qLC=0→(3)
The above relation is in the form of
d2xdt2+ω2x=0→(4)
On comparing (3) and (4) we get
ω2=1LC
ω=1√LC
Topper's Solved these Questions
- II PUC PHYSICS (P.U. BOARD LATEST MODEL QUESTIONS PAPER -2)BOOK - SUNSTAR PUBLICATIONCHAPTER - II PUC PHYSICS (P.U. BOARD LATEST MODEL QUESTIONS PAPER -2)EXERCISE - PART-D
11 Videos
- II PUC PHYSICS (P.U. BOARD LATEST MODEL QUESTIONS PAPER -2)BOOK - SUNSTAR PUBLICATIONCHAPTER - II PUC PHYSICS (P.U. BOARD LATEST MODEL QUESTIONS PAPER -2)EXERCISE - PART-B
8 Videos
- ANNUAL EXAM QUESTION PAPER MARCH-2020BOOK - SUNSTAR PUBLICATIONCHAPTER - ANNUAL EXAM QUESTION PAPER MARCH-2020EXERCISE - Part-D
11 Videos
- II PUC PHYSICS (ANNUAL EXAM QUESTION PAPER MARCH - 2019)BOOK - SUNSTAR PUBLICATIONCHAPTER - II PUC PHYSICS (ANNUAL EXAM QUESTION PAPER MARCH - 2019)EXERCISE - PART - A
37 Videos
Similar Questions
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then

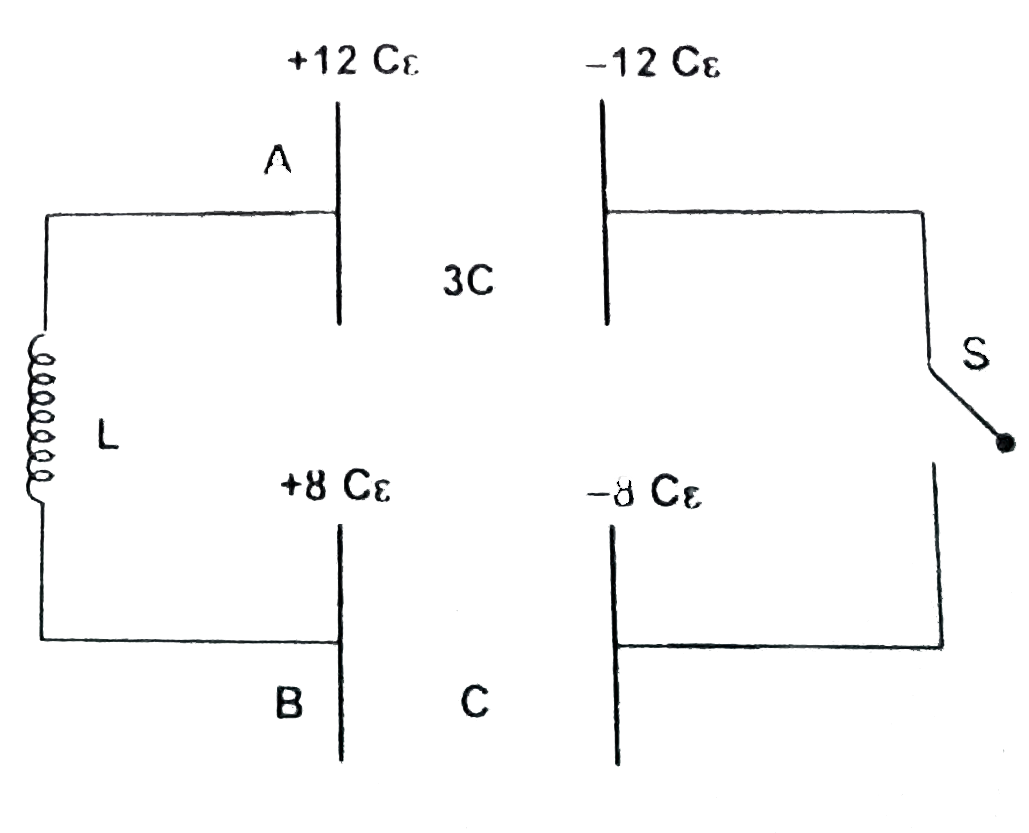
View SolutionIn the adjacent circuit, the capacitor 'A' of capacitance '3C' and the capacitor 'B' of capacitance 'C' are initially charged by potential drops 4ɛ and 8ɛ respectively and connected through and inductor of inductance 'L' with zero initial current as shown. The switch 'S' is closed at t=0. then the maximum current through the inductor is
View Solution
Knowledge Check
In L-C circuit, the charge oscillates with a natural frequency ω0 given by
Aω0=1LCBω0=1√LCCω0=12LCDω0=1√2LCA capacitor of capacitance 4μF is fully charged to a potential difference of 12 V and then charging battery is disconnected. Charged capacitor is now connected across an inductor of self-inductance of 1.2 mH. The current in the circuit at a time when the potential difference across the capacitor is 6 V is
A0.3 AB0.6 AC0.9 AD1.2 AIn the adjacent circuit, the capacitor 'A' of capacitance '3C' and the capacitor 'B' of capacitance 'C' are initially charged by potential drops 4_(varepsilon) and 8ɛ respectively and connected through and inductor of inductance 'L' with zero initial current as shown. The switch 'S' is closed at t=0. then the maximum current through the inductor is
 Aɛ√3CLBɛ√6CLCɛ√12CLDɛ√15CL
Aɛ√3CLBɛ√6CLCɛ√12CLDɛ√15CL
An LC series circuit has an oscillation frequency f. Two isolated inductors, each with inductance L and two capacitors each with capacitance C, all are connected in series and circuit is completed. The oscillation frequency is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View SolutionAn LC series circuit with an inductance L and a capacitance C has an oscillation frequency f. Two isolated induc tors, each with inductance L, and two capacitors, each with capacitance C, are all wired in series and the circuit is com pleted. The oscillation frequency is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
View Solution
