A particle of mass m moves on the x-axis as follows: It starts from rest at r= 0 from the pointr=0, and come to rest at 1 at the point x = 1. The velocity changes lincarly with time. No other information is available about its motion at intermediate times [0<t<1] . If α denotes the instantaneous acceleration of the particle , then
α cannot remain positive for all t in the interval 0 to 1
|α| cannot exceed 2 at any point in its path
|α| must be > 4 some point or points in its path
αmust change sign during the motion, but no other assertion can be made with the given information.
The correct Answer is:A, C
Given x=1 , t2=1
S= Area under velocity -time graph
Vmax=12×Vmax×t2
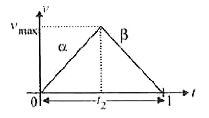
⇒Vmax=2xt2=2m/s
∴α=Vmax−4t22=2−012=4m/s2
∴ In some post or points |α|>4.
Topper's Solved these Questions
- KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type (1 Mark) )
9 Videos
- KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
1 Videos
- KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE WORKOUT ( CATEGORY 2 : Single Option Correct Type (2 Marks))
15 Videos
- HEAT AND THERMAL PHYSICSBOOK - MTG-WBJEECHAPTER - HEAT AND THERMAL PHYSICSEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
15 Videos
- KINETIC THEORY OF GASES BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
7 Videos
Similar Questions
A particle of mass m moves on the x- axis as follows : it starts from rest at t=0, from the point x=0, and comes to rest at t=1 at the point x=1. No other information is available about its motion at intermediate times (0<t<1) . If α denotes the instantaneous accelartion of the particle , then :
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View Solution
Knowledge Check
A particle of mass m moves on the x−aξs as follows : it starts from rest at t=0, from the point x=0, and comes to rest at t=l at the point x=1. No other information is available about its motion at intermediate times (0<t<l) . If α denotes the instantaneous accelartion of the particle , then :
Aα cannot remain positive for all t in the interval 0≤t≤1.B|α| cannot exceed 2 at any point in its path .C|α| must be ≥4 at some point or points in its path .Dα must change sign during the motion , but no other assertion can be made with the information given .A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 A2m/sB3m/sC4m/sD6m/s
A2m/sB3m/sC4m/sD6m/sA point moving along the x- direction starts from rest at x=0 and comes to rest at x=1 after 1 s. Its acceleration at any point is denoted by α . Which of the following is not correct ?
Aα must change sign during the motion.B|α|≥4 units at some or all points during the motion.CIt is not possible to specify an upper limit for |α| from the given data.D|α| cannot be less than 1/2 during the motion.
Starting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionA point moving along the x-direction starts from rest at x=0 and comes to rest at x=1 after 1 s Its accelertion at any point is denoted by α Which of following is not correct ?
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionStarting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View Solution
