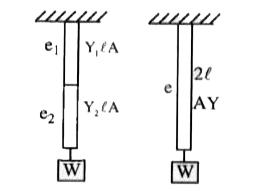
Two wires of same length and radius are joined end to end and loaded. The Young.s modulii of the materials of the two wires are . If the combination behaves as a single wire them its Young.s modulus is
 Solution in Telugu
Solution in Telugu
Similar Questions
An aluminium wire and a steel wire of the same length and cross-section are joined end- to-end. The composite wire is hung from a rigid support and a load is suspen-ded from the free end. If the increase in lengthe of the composite wire is 1.35 mm, find the ratio the (i) stress in the two wires amd (ii) strain in the two wires.
(YAl=0.7×10!1Nm−2,Ysteel=2=1011Nm−2)06:20View SolutionAn aluminium wire and a steel wire of the same length and cross section are joined end to end. The composite wire is hung from a rigid support and a load is suspended from the free end. If the increase in length of the composite wire is 1.35 mm, find the ratio of the i) stress in the two wires and ii) strains in the two wires.
(YAI=7×1010Nm−2,Ysteel=2×1011Nm−2)View SolutionTwo wires of same length and radius are joined in parallel and loaded. The Young.s modulii of the material of the wires are Y1&Y2. If the combination is taken as a single wire them its Young.s modulus is
03:28View SolutionA slightly conical wire of length l and radius r1andr2 is stretched by two forces applied parallel to length in opposite directions and normal to end faces. If Y denotes the Young.s modulus, then find the elongation of the wire.
View SolutionTwo wires A and B have Young's modulii in the ratio 1:2 and ratio of lengths is 1:1. Under the application of same stress the ratio of elongations is
02:18View SolutionTwo wires of same length and thickness are joined end to end. Their Young's moduli are 15×1010pa and 20×1010pa . If the combination is stretched by a certain load, the elongations of these wires will be in the ratio
03:21View SolutionAn iron wire and copper wire having same length and cross-section are suspended from same roof Young.s modulus of copper is 1/3rd that of iron. Then the ratio of the weights to be added at their ends so that their ends are at the same level is
02:59View Solution

