Energy required to ionise 1 model of gaseousHe+ion present in its ground state is
108.8NAeV
13.6eV
54.4 eV
54.4NAeV
The correct Answer is:D
To find the energy required to ionize one mole of gaseous He⁺ ions in their ground state, we can use the formula derived from the Bohr model of the hydrogen-like atoms. Helium ion (He⁺) has a nuclear charge (Z) of +2 since it has two protons.
1. Identify the Formula:
The energy of an electron in a hydrogen-like atom is given by the formula:
En=−Z2⋅RHn2
where:
- En = energy of the electron at level n,
- Z = atomic number (for He⁺, Z = 2),
- RH = Rydberg constant for hydrogen, approximately 13.6eV,
- n = principal quantum number (for ground state, n=1).
2. Substitute Values:
For He⁺ in the ground state (n=1):
E1=−(2)2⋅13.6eV(1)2
E1=−4⋅13.6eV1
E1=−54.4eV
3. Calculate Ionization Energy:
The ionization energy is the energy required to remove the electron from the ground state to infinity (where the energy is 0). Therefore, the ionization energy I is:
I=−E1=54.4eV
4. Convert to Energy per Mole:
To find the energy required to ionize one mole of He⁺ ions, we multiply by Avogadro's number (NA≈6.022×1023):
Imole=54.4eV×6.022×1023mol−1
To convert eV to joules (1 eV = 1.602×10−19J):
Imole=54.4×1.602×10−19J×6.022×1023
Imole≈5.22×103J/mol
Final Answer:
The energy required to ionize one mole of gaseous He⁺ ions in their ground state is approximately 5220 J/mol.
The energy of an electron in a hydrogen-like atom is given by the formula:
En=−Z2⋅RHn2
where:
- En = energy of the electron at level n,
- Z = atomic number (for He⁺, Z = 2),
- RH = Rydberg constant for hydrogen, approximately 13.6eV,
- n = principal quantum number (for ground state, n=1).
For He⁺ in the ground state (n=1):
E1=−(2)2⋅13.6eV(1)2
E1=−4⋅13.6eV1
E1=−54.4eV
The ionization energy is the energy required to remove the electron from the ground state to infinity (where the energy is 0). Therefore, the ionization energy I is:
I=−E1=54.4eV
To find the energy required to ionize one mole of He⁺ ions, we multiply by Avogadro's number (NA≈6.022×1023):
Imole=54.4eV×6.022×1023mol−1
To convert eV to joules (1 eV = 1.602×10−19J):
Imole=54.4×1.602×10−19J×6.022×1023
Imole≈5.22×103J/mol
The energy required to ionize one mole of gaseous He⁺ ions in their ground state is approximately 5220 J/mol.
Topper's Solved these Questions
Similar Questions
Energy required to ionise 2 mole of gaseous He+ ion present in its ground state is :
View SolutionThe amount of energy required to remove the electron from a Li2+ ion in its ground state is , how many times greater than the amount of energy required to remove the electron from a H-atom in its ground state ?
View Solution
Knowledge Check
The ionisation energy (IE1) of an atom is defined as the energy needed to remove an electron from gaseous atom in its ground state. The 2nd ionisation energy (IE2) is the additional energy needed to remove the 2nd electron and so on. The successive ionisation energy of any species is increasing always.
In the graph below elements of period given with their ionisation energy. Select the one which represents an alkali metal:
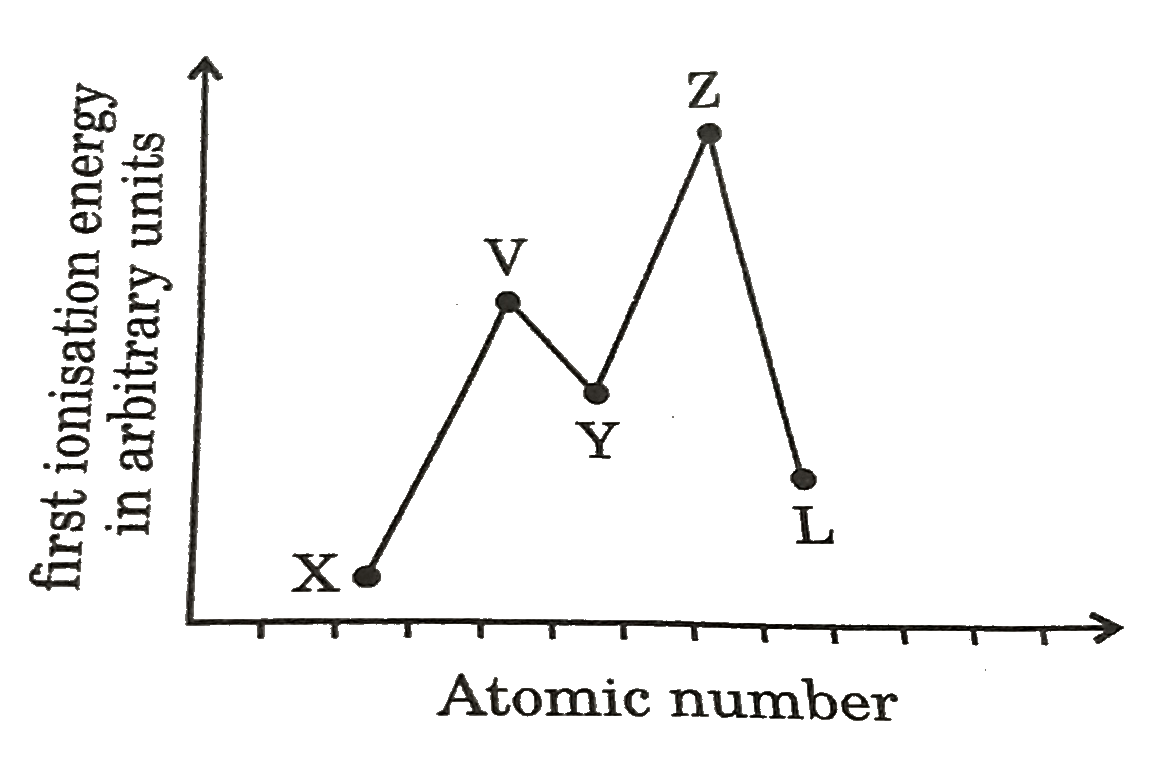 AXBYCZDL
AXBYCZDLThe ionisation energy (IE1) of an atom is defined as the energy needed to remove an electron from gaseous atom in its ground state. The 2nd ionisation energy (IE2) is the additional energy needed to remove the 2nd electron and so on. The successive ionisation energy of any species is increasing always.
Generally, the first ionisation energy increase along a period. But there are some exceptions. One which is not an exception is:AN and OBNa and MgCMg and AIDBe and BThe ionisation energy (IE1) of an atom is defined as the energy needed to remove an electron from gaseous atom in its ground state. The 2nd ionisation energy (IE2) is the additional energy needed to remove the 2nd electron and so on. The successive ionisation energy of any species is increasing always.
Which represents the correct order of first ionisation potential of third period elements?ANa>Mg>Ai>SiBNa<Mg<AI<SiCNa<Si<AI<MgDNa<AI<Mg<Si
The energy required to remove an electron from an isolated gaseous atom in its ground state is called ionisation enthalpy.From the following, select the element having maximum value of 2nd ionization enthalpy.
Be
C
N
O
View SolutionThe minimum energy required to excite a hydrogen atom from its ground state is ______.
View Solution" How many unpaired electrons are present in a gaseous Co+3 ion in its ground state? "
View SolutionThe ionisation energy of hydrogen atom is 1.312×106Jmol−1. Calculate the energy required to excite an electron in a hydrogen atom from the ground state to the first excited state.
View SolutionIn a hydrogen like atom, energy required to excite the electron from its first excited state to second excited state is 7.55 eV. The energy required to remove the electron from its ground state is
View Solution
