The lattice enthalpy of KI will be, if the enthalpy of (I) Δ H− (KI) = -78.0 kcal mol−1 (II) Ionisation energy of K to K+ is 4.0 eV (III) Dissociation energy of I2 is 28.0 kcal mol−1 (IV) Sublimation energy of K is 20.0 kcal mol−1 (V) electron gain enthalpy forI to I− is -70.0 kcal mol−1 (VI) Sublimation energy of I2 is 14.0 kcal mol−1 (1 eV =23. 0 kcal mol^-1)
+14.1kJmol−1
−14.1kJmol−1
−141kJmol−1
+141kJmol−1
The correct Answer is:C
To calculate the lattice enthalpy of potassium iodide (KI), we can use the Born-Haber cycle, which relates the lattice enthalpy to various other thermodynamic quantities. The formula we will use is:
ΔHreaction=ΔHsublimation(K)+ΔHionization(K)+ΔHdissociation(I2)+ΔHelectron gain(I)+ΔHlattice
Where:
- ΔHreaction is the enthalpy of formation of KI, which is given as -78.0 kcal/mol.
- ΔHsublimation(K) is the sublimation energy of potassium, given as 20.0 kcal/mol.
- ΔHionization(K) is the ionization energy of potassium, which is given as 4.0 eV. We need to convert this to kcal/mol using the conversion factor 1 eV=23.0 kcal/mol:
ΔHionization(K)=4.0 eV×23.0 kcal/eV=92.0 kcal/mol
- ΔHdissociation(I2) is the dissociation energy of iodine, given as 28.0 kcal/mol. Since we are dealing with I2, we need to divide this by 2 to get the energy for one mole of iodine atoms:
ΔHdissociation(I)=28.0 kcal/mol2=14.0 kcal/mol
- ΔHelectron gain(I) is the electron gain enthalpy for iodine, given as -70.0 kcal/mol.
Now, we can substitute these values into the equation:
−78.0 kcal/mol=20.0 kcal/mol+92.0 kcal/mol+14.0 kcal/mol−70.0 kcal/mol+ΔHlattice
Now, let's simplify the right side:
−78.0 kcal/mol=20.0+92.0+14.0−70.0+ΔHlattice
−78.0 kcal/mol=56.0+ΔHlattice
Now, we can isolate ΔHlattice:
ΔHlattice=−78.0 kcal/mol−56.0 kcal/mol
ΔHlattice=−134.0 kcal/mol
Thus, the lattice enthalpy of KI is −134.0 kcal/mol.
- ΔHreaction is the enthalpy of formation of KI, which is given as -78.0 kcal/mol.
- ΔHsublimation(K) is the sublimation energy of potassium, given as 20.0 kcal/mol.
- ΔHionization(K) is the ionization energy of potassium, which is given as 4.0 eV. We need to convert this to kcal/mol using the conversion factor 1 eV=23.0 kcal/mol:
ΔHionization(K)=4.0 eV×23.0 kcal/eV=92.0 kcal/mol
- ΔHdissociation(I2) is the dissociation energy of iodine, given as 28.0 kcal/mol. Since we are dealing with I2, we need to divide this by 2 to get the energy for one mole of iodine atoms:
ΔHdissociation(I)=28.0 kcal/mol2=14.0 kcal/mol
- ΔHelectron gain(I) is the electron gain enthalpy for iodine, given as -70.0 kcal/mol.
−78.0 kcal/mol=56.0+ΔHlattice
ΔHlattice=−134.0 kcal/mol
Topper's Solved these Questions
Similar Questions
Find the electron affinity of chlorine from the following data. Enthalpy of formation of LiCI is −97.5kcalmol−1, lattice energy of LiCI=−197.7kcalmol−1. Dissociation energy of chlirine is 57.6kcalmol−1, sublimation enthalpy of lithium =+38.3kcalmol−1, ionisation energy of lithium =123.8kcalmol−1.
View SolutionHeat of hydrogention of
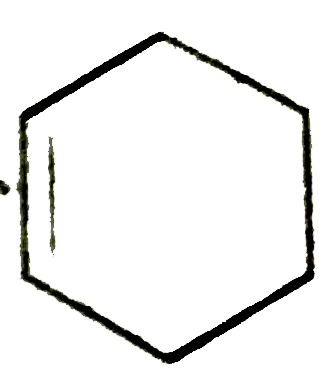is 29 kcal mol−1 and that of 
is 56kcalmol−1. Calculate the resonance energy of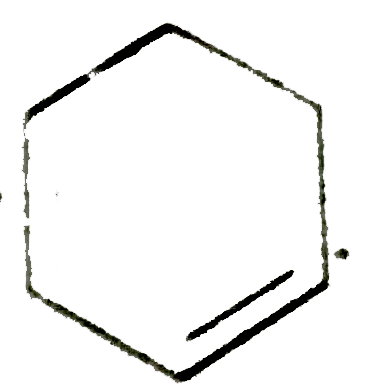 
View Solution
Knowledge Check
The lattice enthalpy of KI will be, if the enthalpy of (I) Δ H− (KI) = -78.0 kcal mol−1 (II) Ionisation energy of K to K+ is 4.0 eV (III) Dissociation energy of I2 is 28.0 kcal mol−1 (IV) Sublimation energy of K is 20.0 kcal mol−1 (V) electron gain enthalpy forI to I− is -70.0 kcal mol−1 (VI) Sublimation energy of I2 is 14.0 kcal mol−1 (1 eV =23. 0 kcal mol^-1)
A+14.1kJmol−1B−14.1kJmol−1C−141kJmol−1D+141kJmol−1The bond energy of H2 is 104.3kcalmol−1 . If means that :
A104.3kcalheat is needed to break up 'N' bonds in N molecules of H2.B104.3kcal heat is needed to break up 6.023×1023 molecules into 1.2046×1024 atoms of HC104.3kcal heat is evolved during combination of 2N atoms of H to form N molecules of H2.Dall of theseThe bond energy of H2 is 104.3k.calmol−1. It means that
A104.3 K. cal heat is released during breaking up 'N' bonds in N molecules of H2B104.3 K. cal heat is needed to break up 6.023×1023 molecules into 1.2046×1024 ayoms of HC104.3 K. cal heat is evolved during combination of 2N atoms of H to form N molecules of H2DBoth 2 and 3.
If enthalpy of formation of Cl4 is 316 kcal mol−1 the dissociation energy of C−Cl is
View SolutionThe dissociation energy of CH4(g) is 360 kcal mol−1 and that of C2H6(g)is620kcalmol−1. The C-C bond energy
View SolutionResonance energy of benzene is 36kcalmol−1. This means
View SolutionThe enthalpy of formation of UF(g) is 22 kcal mol−1 and that of U(g) is 128 kcal mol−1. The bond energy of the F-F bond is 37.0 kcal mol−1. The bond dissociation energy of UF(g) is/are.
View SolutionThe enthalpy of formation of UF(g) is 22 kcal mol−1 and that U(g) is 128 kcal mol−1. The bond energy of the F-F bond is 37.0 kcal mol−1. The bond dissociation energy of UF(g) is/are:
View Solution