A crystal is made up of particles A. B and C. A forms fcc packing, B occupies all octahedral voids and C occupies all tetrahedral voids. If all the particles along one body diagonal are removed, then the formula of the crystal would be
The correct Answer is:D
To solve the problem, we need to determine the new formula of the crystal after removing the particles along one body diagonal. Let's break it down step by step.
Step 1: Determine the number of particles A in the FCC structure.
- In a face-centered cubic (FCC) lattice, there are 4 atoms of A per unit cell.
- These atoms are located at the corners and face centers of the cube.
Hint: Remember that in an FCC structure, each corner atom contributes 1/8 to the unit cell and each face-centered atom contributes 1/2.
Step 2: Identify the particles removed along the body diagonal.
- The body diagonal of a cube connects two opposite corners.
- In a cube, there are 8 corners, and along the body diagonal, we will remove 2 corner atoms.
Hint: Visualize the cube and identify the corners that lie on the body diagonal.
Step 3: Calculate the contribution of the removed corner atoms.
- Each of the 2 corner atoms removed contributes 1/8 to the unit cell.
- Therefore, the total contribution of the removed corner atoms is:
2×18=28=14
Step 4: Calculate the remaining number of A atoms.
- Initially, there were 4 A atoms in the FCC unit cell.
- After removing the contribution from the body diagonal:
Remaining A=4−14=164−14=154
Hint: Always keep track of the contributions when atoms are removed from a crystal structure.
Step 5: Determine the number of B atoms in the octahedral voids.
- In an FCC structure, there are 4 octahedral voids (OHV) per unit cell.
- Since we are removing atoms along the body diagonal, we need to consider how many octahedral voids are affected.
- After the removal, there will be 3 octahedral voids remaining.
Hint: Remember that the octahedral voids are located at the center of the cube and at the edge centers.
Step 6: Determine the number of C atoms in the tetrahedral voids.
- In an FCC structure, there are 8 tetrahedral voids (THV) per unit cell.
- Each body diagonal has 2 tetrahedral voids that will be removed.
- Therefore, the remaining number of tetrahedral voids is:
8−2=6
Hint: Tetrahedral voids are located at specific positions relative to the atoms in the FCC structure.
Step 7: Write the new formula of the crystal.
- Now we have:
- A: 154
- B: 3
- C: 6
- To simplify, we can multiply all coefficients by 4 to eliminate the fraction:
A:15,B:12,C:24
- The simplified formula becomes:
A15B12C24
Hint: Always check if the coefficients can be simplified further.
Final Answer:
The formula of the crystal after removing the particles along one body diagonal is A15B12C24.
- In a face-centered cubic (FCC) lattice, there are 4 atoms of A per unit cell.
- These atoms are located at the corners and face centers of the cube.
- The body diagonal of a cube connects two opposite corners.
- In a cube, there are 8 corners, and along the body diagonal, we will remove 2 corner atoms.
- Each of the 2 corner atoms removed contributes 1/8 to the unit cell.
- Therefore, the total contribution of the removed corner atoms is:
2×18=28=14
- Initially, there were 4 A atoms in the FCC unit cell.
- After removing the contribution from the body diagonal:
Remaining A=4−14=164−14=154
- In an FCC structure, there are 4 octahedral voids (OHV) per unit cell.
- Since we are removing atoms along the body diagonal, we need to consider how many octahedral voids are affected.
- After the removal, there will be 3 octahedral voids remaining.
- In an FCC structure, there are 8 tetrahedral voids (THV) per unit cell.
- Each body diagonal has 2 tetrahedral voids that will be removed.
- Therefore, the remaining number of tetrahedral voids is:
8−2=6
- Now we have:
- A: 154
- B: 3
- C: 6
A:15,B:12,C:24
A15B12C24
The formula of the crystal after removing the particles along one body diagonal is A15B12C24.
Topper's Solved these Questions
Similar Questions
A crystal is made of particles X,Y and Z.X form fcc packing . Y occupies all the octahedral void of X and Z occupies all the tetrahedral voids of X . If all the particles along one body diagonal are removed then the formula of the crystal would be:
View SolutionA forms ccp lattice B occupy half of the octahedral voids and O occupy all the tetrahedral voids. Calculate formula-
View Solution
Knowledge Check
A crystal is made up of particals X, Y, and Z. X froms f packing. Y occupies all octahedral voids of X and Z occupies all tetrahedral voids of X. If all the particles along one body diagonal are removed. Then the fromula of the crystal would be
AXYZ2BX2YZ2CX8Y4Z5DX5Y4Z8A crystal is made of particle X,Y and Z 'X' forms +FCC packing+. 'Y' occupies all the octahedral voids of X and Z occupies all tetrahedral voiods of X. If all the particles along one body diagonal are removed, then the formula of the crystal would be?
AXYZ2BX2YZ2CX8Y4Z5Dnone of theseA crystal is made of particles X and Y. X forms FCC packing and Y occupies all the octahedral voids. Find the formula of the crystal if all the particles along one body diagonal are removed.
AX4Y3BX5Y4CX5Y5DNone of these
In a crystalline solid, atom of A form fcc packing and atoms of B occupy all octahedral voids. If all the atoms along one body diagonal are removed then what will be the simplest formula of the crystalline solid ?
View SolutionA crystal is made of particles X and Y.X form fcc packing and Y occupies all the octahedral voids . If all the particles along one body diagonal are removed then the formula of the crystal would de :
View SolutionA crystal is made of particles A and B. A forms FCC packing and B occupies all the octahedral voids. If all the particles along the plane as shown in figure are removed, then the formula of the crystal would be :
View SolutionA forms ccp lattice B occupy half of the octahedral voids and O occupy all the tetrahedral voids. Calculate formula-
View SolutionA crystal is made of particles A and B . From fcc packing and B occupies all the octahedral voids . If all the particle along the plane as shown in figure are removed , then, the formula of the crystal would be :
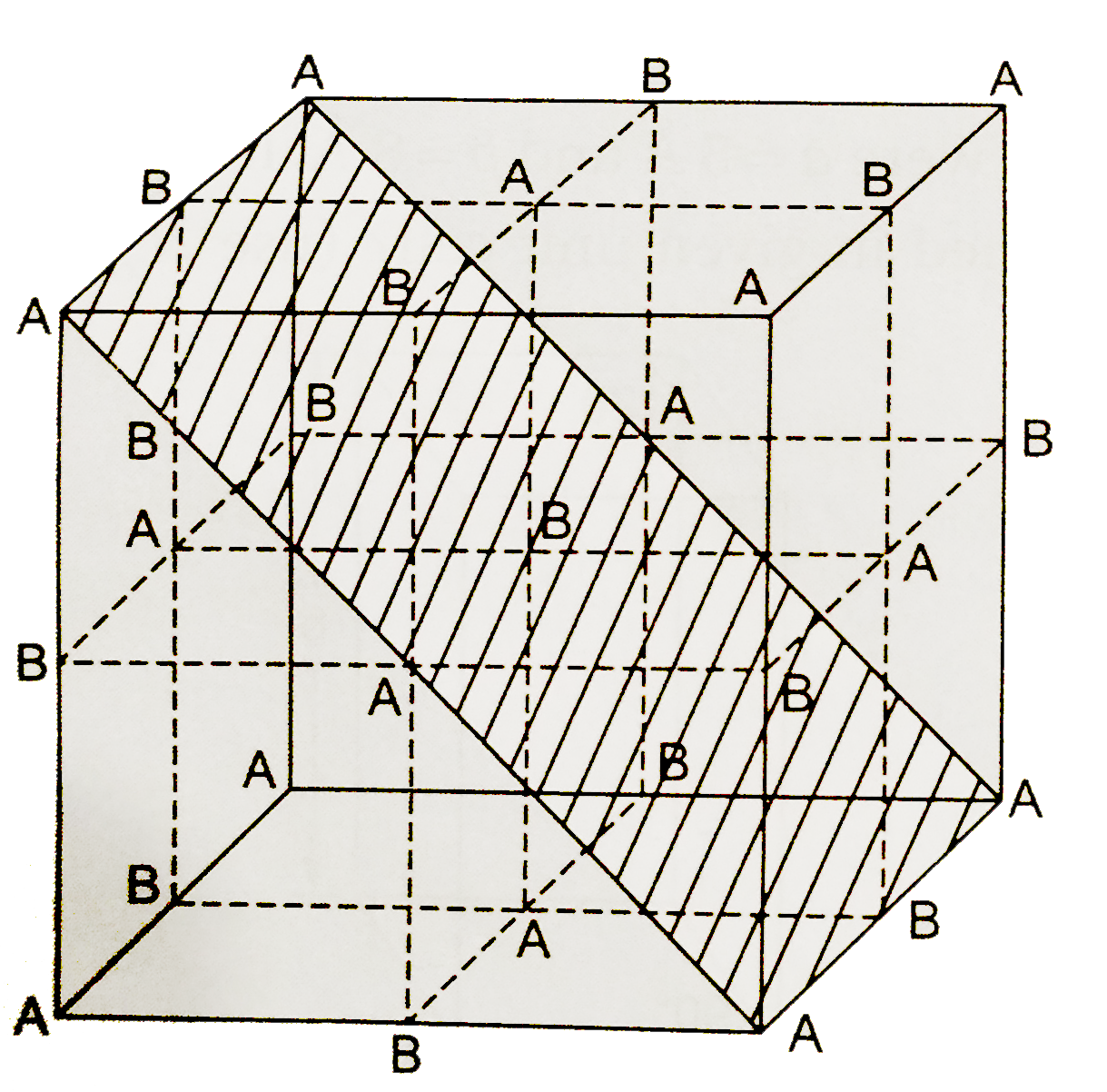
View Solution
