For a reaction, activation energy (Ea) =0 and rate constant, k=1.5x104s−1 at 300 K. What is the value of rate constant at 320 K'?
3.2x106s−1
3.2x104s−1
1.5x104s−1
6.4x108s−1
The correct Answer is:C
To solve the problem, we will use the Arrhenius equation, which relates the rate constants at two different temperatures. The equation is given by:
ln(k2k1)=−EaR(1T2−1T1)
Where:
- k1 is the rate constant at temperature T1
- k2 is the rate constant at temperature T2
- Ea is the activation energy
- R is the universal gas constant (approximately 8.314J/mol⋅K)
- T1 and T2 are the absolute temperatures in Kelvin
Step 1: Identify the given values
- Ea=0kJ/mol (activation energy)
- k1=1.5×104s−1 at T1=300K
- T2=320K
Step 2: Substitute the values into the Arrhenius equation
Since the activation energy Ea=0, the equation simplifies to:
ln(k2k1)=−0R(1T2−1T1)
This simplifies to:
ln(k2k1)=0
Step 3: Solve for k2
Taking the exponential of both sides gives:
k2k1=e0=1
Thus, we have:
k2=k1
Step 4: Substitute k1 to find k2
Since k1=1.5×104s−1:
k2=1.5×104s−1
Final Answer:
The value of the rate constant at 320K is:
k2=1.5×104s−1
- k1 is the rate constant at temperature T1
- k2 is the rate constant at temperature T2
- Ea is the activation energy
- R is the universal gas constant (approximately 8.314J/mol⋅K)
- T1 and T2 are the absolute temperatures in Kelvin
- Ea=0kJ/mol (activation energy)
- k1=1.5×104s−1 at T1=300K
- T2=320K
Since the activation energy Ea=0, the equation simplifies to:
Taking the exponential of both sides gives:
Since k1=1.5×104s−1:
The value of the rate constant at 320K is:
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - MOCK_TEST_17EXERCISE - Example22videos
MOCK_TEST_17
- BOOK - AAKASH INSTITUTECHAPTER - ORGANIC CHEMISTRY : SOME BASIC PRINCIPLES AND TECHNIQUES EXERCISE - Assignment(Section-D)(Assertion - Reason Type Questions)12videos
ORGANIC CHEMISTRY : SOME BASIC PRINCIPLES AND TECHNIQUES
Similar Questions
Knowledge Check
- Question 1 - Select One
For a reaction the activation energy Ea=0 and the rate constant=3.2×106sec−1 at 300K. What is the value of rate constant at 310K?
A3.2×10−12s−1B3.2×10−6s−1C6.4×1012s−1D6.4×106s−1 - Question 2 - Select One
For a reaction the activation energy Ea=0 and the rate constant=3.2×106sec−1 at 300K. What is the value of rate constant at 310K?
A3.2×10−12s−1B3.2×106s−1C6.4×1012s−1D6.4×106s−1 - Question 3 - Select One
For a reaction the activation energy Ea=0 and the rate constant=3.2×106sec−1 at 300K. What is the value of rate constant at 310K?
A6.4×106sec−1B6.4×1012sec−1C3.2×106sec−1D0
Rate constant of a first order reaction at 298 K is 15.5s−1. What is the approximate rate constant for this reaction at 308 K?
View SolutionThe decomposition of phosphine,
4PH3(g)→P4(g)+6H2(g) has rate law , Rate = k[PH3]. The rate constant is 6.0×10−4s−1 at 300 K and activation energy is 3.05×105 J mol−1. Calculate the value of the rate constant at 310 K (R=8.314JK−1mol−1)View SolutionThe activation energy of a reaction is zero. Its rate constant at 280 K is 16×10−6s−1 the rate constant at 300k is
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
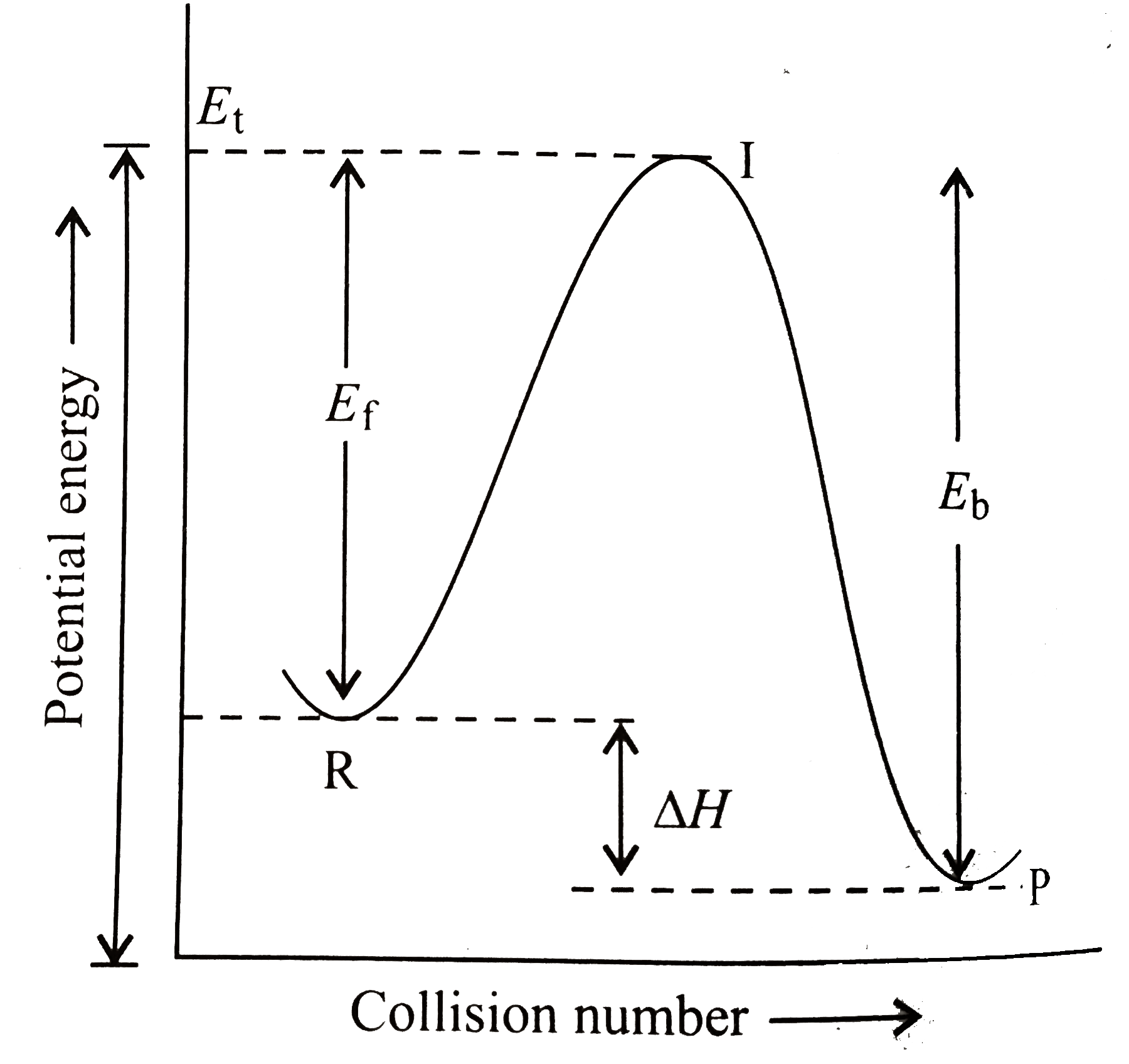
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, thenView SolutionA reaction has a rate constant k=8.54×10−4Ms−1 at 45∘ C and an activation energy, Ea=90.8KJ . What is the value of K at 25∘ C?
View Solution

