The acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
4 m/s
2 m/s
6 m/s
Infinity
The correct Answer is:B
To find the maximum velocity of a particle moving along a straight line with the given acceleration a=4−2v, where v is the speed of the particle, we can follow these steps:
1. Understand the relationship between acceleration and velocity:
The acceleration a can be expressed in terms of velocity v as:
a=dvdt=4−2v
2. Rearrange the equation:
Rearranging the equation gives:
dv4−2v=dt
3. Integrate both sides:
We will integrate the left side with respect to v and the right side with respect to t:
∫dv4−2v=∫dt
The left side can be simplified using substitution. Let u=4−2v, then du=−2dv or dv=−du2:
∫−12duu=∫dt
This gives:
−12ln|4−2v|=t+C
4. Solve for v:
Rearranging the equation, we get:
ln|4−2v|=−2t−2C
Exponentiating both sides results in:
4−2v=e−2t−2C
Let K=e−2C, then:
4−2v=Ke−2t
Thus:
2v=4−Ke−2t
Therefore:
v=2−K2e−2t
5. Find the maximum velocity:
As t approaches infinity, e−2t approaches 0. Thus:
vmax=2−K2⋅0=2
6. Conclusion:
The maximum velocity of the particle is:
vmax=2m/s
The acceleration a can be expressed in terms of velocity v as:
a=dvdt=4−2v
Rearranging the equation gives:
dv4−2v=dt
We will integrate the left side with respect to v and the right side with respect to t:
∫dv4−2v=∫dt
The left side can be simplified using substitution. Let u=4−2v, then du=−2dv or dv=−du2:
∫−12duu=∫dt
This gives:
−12ln|4−2v|=t+C
Rearranging the equation, we get:
ln|4−2v|=−2t−2C
Exponentiating both sides results in:
4−2v=e−2t−2C
Let K=e−2C, then:
4−2v=Ke−2t
Thus:
2v=4−Ke−2t
Therefore:
v=2−K2e−2t
As t approaches infinity, e−2t approaches 0. Thus:
vmax=2−K2⋅0=2
The maximum velocity of the particle is:
vmax=2m/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
Velocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
A3π[2−√32]B[2−√32]C2π[2−√32]D4π[2−√32]The acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
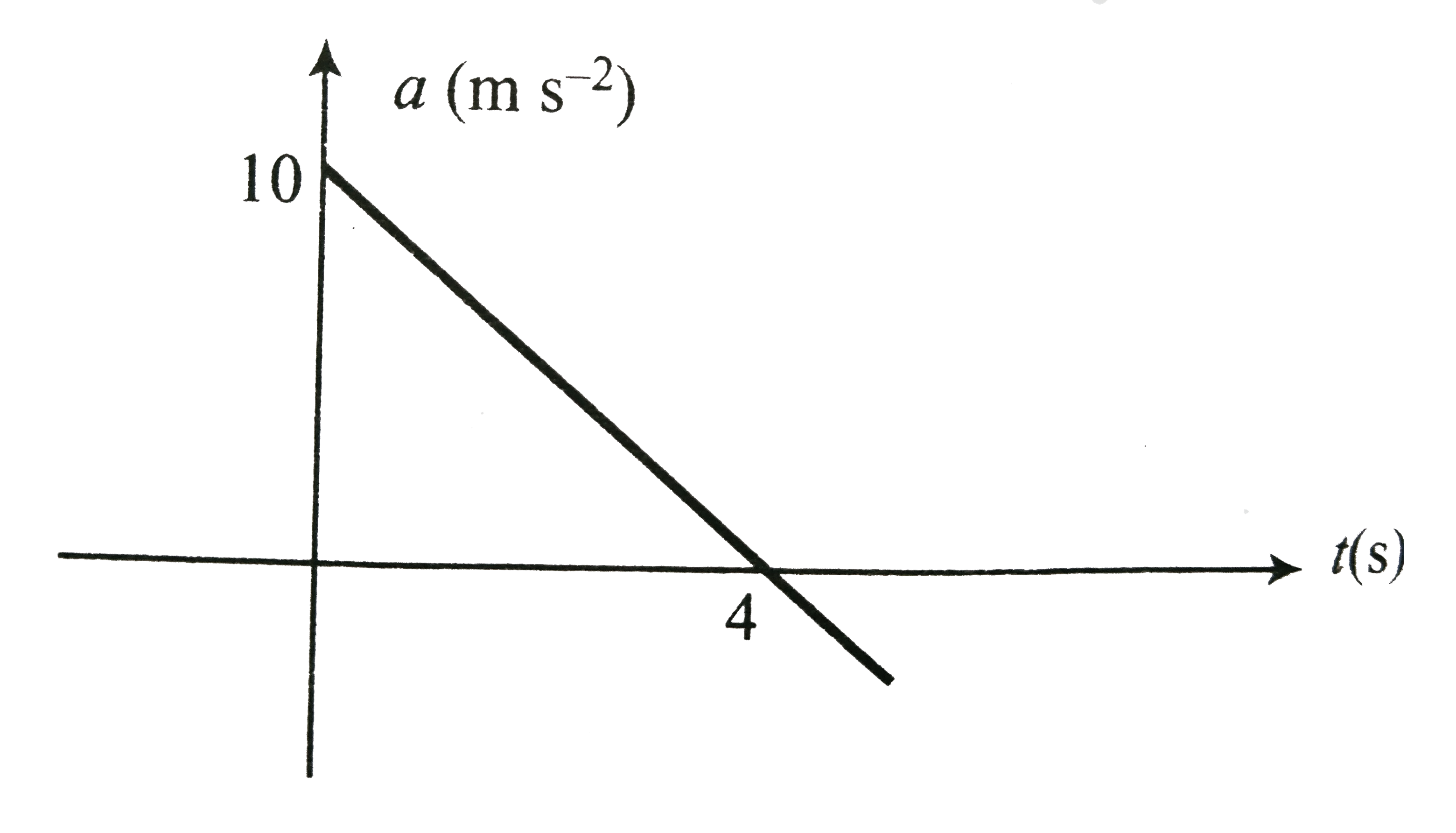 .A12sB5sC8sD16s
.A12sB5sC8sD16sAt any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
Av>0,a>0Bv<0,a>0Cv>0,a<0Dv>0,a=0
The coordinates of a moving particle at any time t are given by x = ct and y = bt. The speed of the particle at time t is given by
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionThe coordinates of a moving particle at any time t are given by x=αt3 and y=βt3. The speed of the particle at time t is given by
View SolutionThe coordinates of a moving particle at any time 't' are given by x=αt and y=βt. The speed of the particle at time 't' is given by
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View Solution
