A particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
5ms2
10ms2
50ms2
100ms2
The correct Answer is:B
To find the acceleration of the particle, we can use the formula from the first equation of motion:
V=U+A⋅T
Where:
- V = final velocity
- U = initial velocity
- A = acceleration
- T = time
1. Identify the given values:
- Initial velocity, U=0m/s (since the particle starts from rest)
- Final velocity, V=50m/s
- Time, T=5s
2. Substitute the known values into the equation:
50=0+A⋅5
3. Simplify the equation:
50=A⋅5
4. Solve for acceleration A:
A=505
A=10m/s2
Final Answer:
The acceleration of the particle is 10m/s2.
---
- V = final velocity
- U = initial velocity
- A = acceleration
- T = time
- Initial velocity, U=0m/s (since the particle starts from rest)
- Final velocity, V=50m/s
- Time, T=5s
50=0+A⋅5
50=A⋅5
A=505
A=10m/s2
The acceleration of the particle is 10m/s2.
Topper's Solved these Questions
Similar Questions
A particle starts from rest with acceleration 2m/s2. The acceleratioin of the particle of the particle descreases down to zero uniformly during time -interval of 4s. The velocity of particle after 2s is
View SolutionA train starting from rest attains a velocity of 72km/h in 5 minutes . Assuming that the acceleration is uniform , find (i) the acceleration and (ii) the distance travelled by the train for attaining this velocity .
View Solution
Knowledge Check
Starting from a stationary position, Sunil moves his car to attain a velocity of 20ms−1 in 10s. Find the acceleration of the car.
A2ms1B2ms−2C2ms−1D2ms2A particle starts from the origin with a velocity of 10ms−1 and moves with a constant acceleration till the velocity increases to 50ms−1. At that instant, the acceleration is suddenly reversed. What will be the velocity of the particle, when it returne to the starticng point?
AZeroB10ms−1C50ms−1D70ms−1A particle starts moving in +ve x direction with initial velocity of 10ms−1 with a uniform acceleration of magnitude 2ms−2 but directed in -ve x direction. What is the distance traversed by the particle in 12 seconds:
A−24mB24mC70mD74m
A particle is moving with an intial velocity of 5ms−1. What will be the velocity of the particle at t=3s, if the acceleration of the particle is given by
a=16t3−12t2+6t−25
View SolutionParticle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
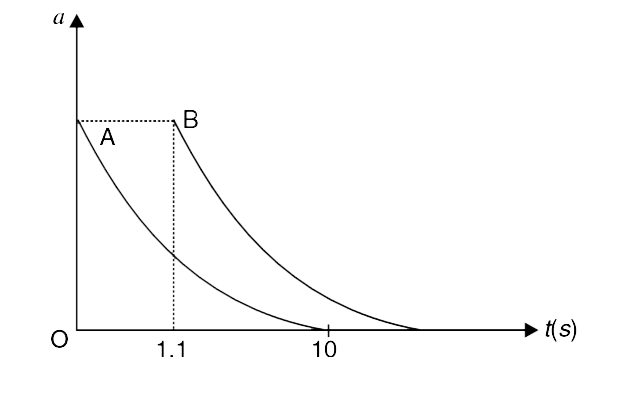
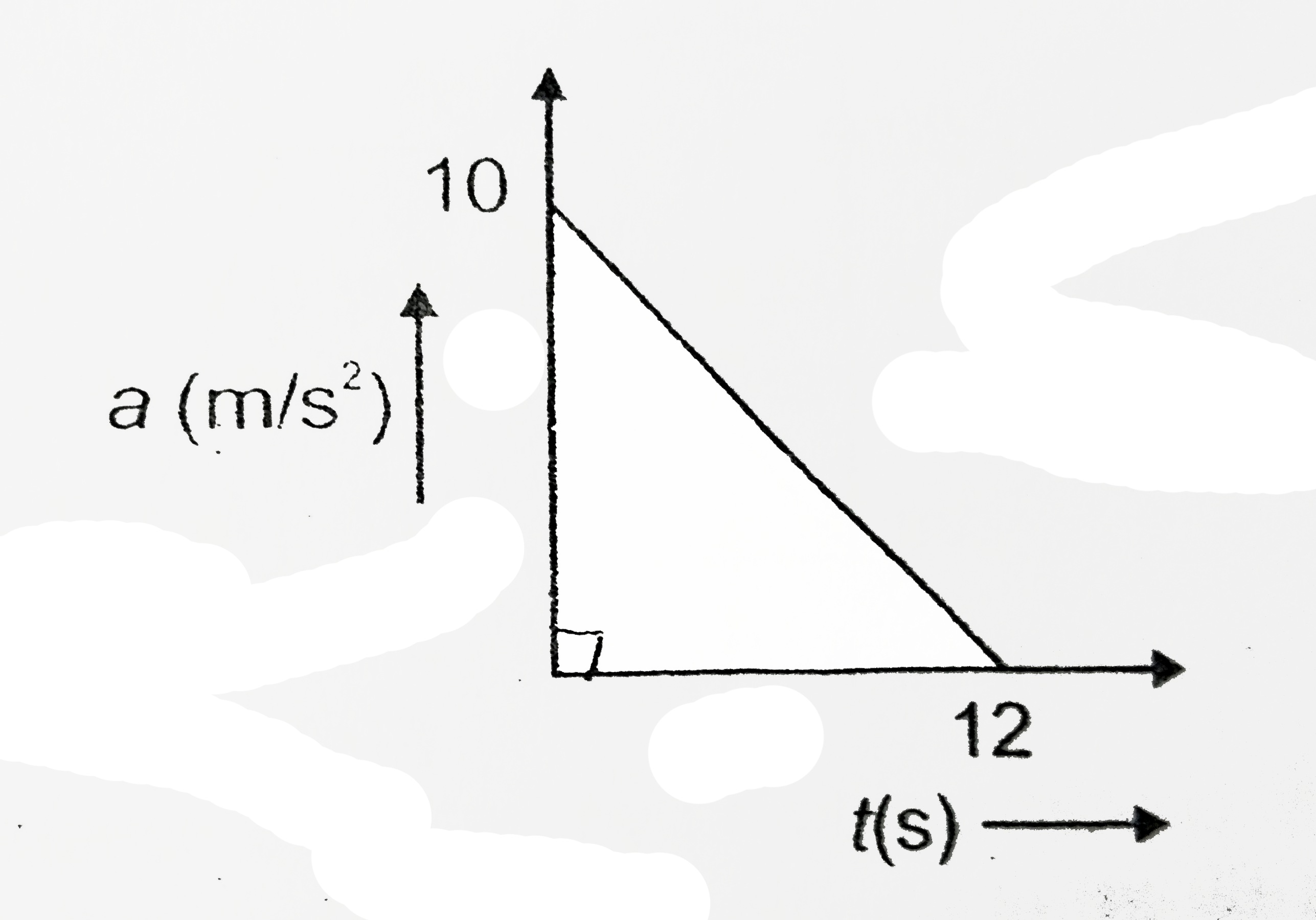
View SolutionA particle starting from rest undergoes a rectilinear motion with acceleration a. The variation of a with time t is shown below. The maximum velocity attained by the particle during its motion is
View SolutionThe acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c. The velocity of the particle after time t will be :
View SolutionA particle moves in the direction of east for 2s with velocity of 15ms−1. Then it moves towards north for 8s with a a velocity of 5ms−1. The average velocity of the particle is
View Solution
