If two projectile of same mass are thrown at an angle of 50° and 40° with the horizontal with the same speed then, which of the following statement is true?
Time of flight of both projectile is same
Maximum height acquired by both projectiles is same
Horizontal range of both projectiles is Same
None of these
The correct Answer is:C
To solve the problem, we need to analyze the projectile motion of two objects thrown at different angles but with the same initial speed. We will evaluate the time of flight, maximum height, and horizontal range for both projectiles.
1. Understanding the Problem:
We have two projectiles thrown at angles of 50° and 40° with the same initial speed (u). We need to determine which statement regarding their motion is true.
2. Time of Flight:
The formula for the time of flight (T) of a projectile is given by:
T=2usinθg
where g is the acceleration due to gravity. Since the angles (50° and 40°) are different, the sine values will also be different. Thus, the time of flight for both projectiles will not be the same.
Conclusion: The time of flight for both projectiles is not the same.
3. Maximum Height:
The formula for the maximum height (H) reached by a projectile is:
H=u2sin2θ2g
Similar to the time of flight, since the angles are different, the sine values will differ. Therefore, the maximum heights for both projectiles will also be different.
Conclusion: The maximum height acquired by both projectiles is not the same.
4. Horizontal Range:
The formula for the horizontal range (R) of a projectile is:
R=u2sin2θg
Here, we need to evaluate sin2θ for both angles:
- For θ1=50°:
sin2θ1=sin100°
- For θ2=40°:
sin2θ2=sin80°
We know that:
sin100°=sin(90°+10°)=cos10°andsin80°=sin(90°−10°)=cos10°
Therefore, sin100°=sin80°. This means:
R1=R2
Hence, the horizontal range for both projectiles is the same.
Conclusion: The horizontal range for both projectiles is the same.
Final Answer:
The correct statement is that the horizontal range for both projectiles is the same.
---
We have two projectiles thrown at angles of 50° and 40° with the same initial speed (u). We need to determine which statement regarding their motion is true.
The formula for the time of flight (T) of a projectile is given by:
T=2usinθg
where g is the acceleration due to gravity. Since the angles (50° and 40°) are different, the sine values will also be different. Thus, the time of flight for both projectiles will not be the same.
The formula for the maximum height (H) reached by a projectile is:
H=u2sin2θ2g
Similar to the time of flight, since the angles are different, the sine values will differ. Therefore, the maximum heights for both projectiles will also be different.
The formula for the horizontal range (R) of a projectile is:
R=u2sin2θg
Here, we need to evaluate sin2θ for both angles:
- For θ1=50°:
sin2θ1=sin100°
- For θ2=40°:
sin2θ2=sin80°
sin100°=sin(90°+10°)=cos10°andsin80°=sin(90°−10°)=cos10°
Therefore, sin100°=sin80°. This means:
R1=R2
Hence, the horizontal range for both projectiles is the same.
The correct statement is that the horizontal range for both projectiles is the same.
Topper's Solved these Questions
Similar Questions
A ball of mass 2kg is thrown with velocity 10ms at an angle of 30°to the horizontal and another ball with the same mass is thrown at an angel of 60° to the horizontal with the same speed.The ratio will be their range will be
View SolutionShow that there are two angles of projection for which the horizontal range is the same.
View Solution
Knowledge Check
Two binary solutions have the same molarity. Which of the following statements is true?
AEqual volumes of the two solutions contain equal number of solute molecules.BEqual weights of the two solutions contain equal number of solute molecules.CThe two solutions, must have the same molality.DThe two solutions must have the same mole fraction.Two projectiles of same mass and with same velocity are thrown at an angle 60∘ and 30∘ with the horizontal, then which quantity will remain same:-
Atime of flightBrange of projectileCmax height acquiredDall of themTwo projectiles A and B are projected with same speed at an angle 30∘ and 60∘ to the horizontal, then which of the following is not valid where T is total time of flight, H is max height and R is horizontal range.
AHA=3HBBTB=√3TACRA=RBDHB−3HA
A sphere is projected horizontally with a speed v from the edge of a table of height h above a level horizontal floor. At the same instant, another sphere is released from the edge of the same table. Identify which of the following statements is true?
View SolutionTwo projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
View SolutionThree projectile A, B and C ar thrown from the same point in the same plane. Their trajectories are shown in the figure, Then which of the following statement is true -
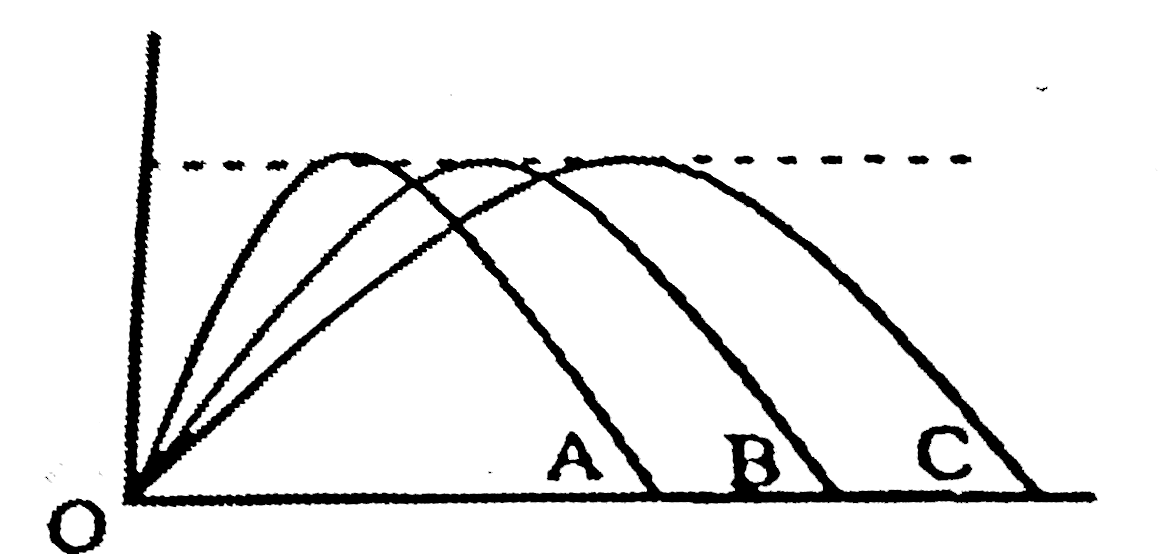
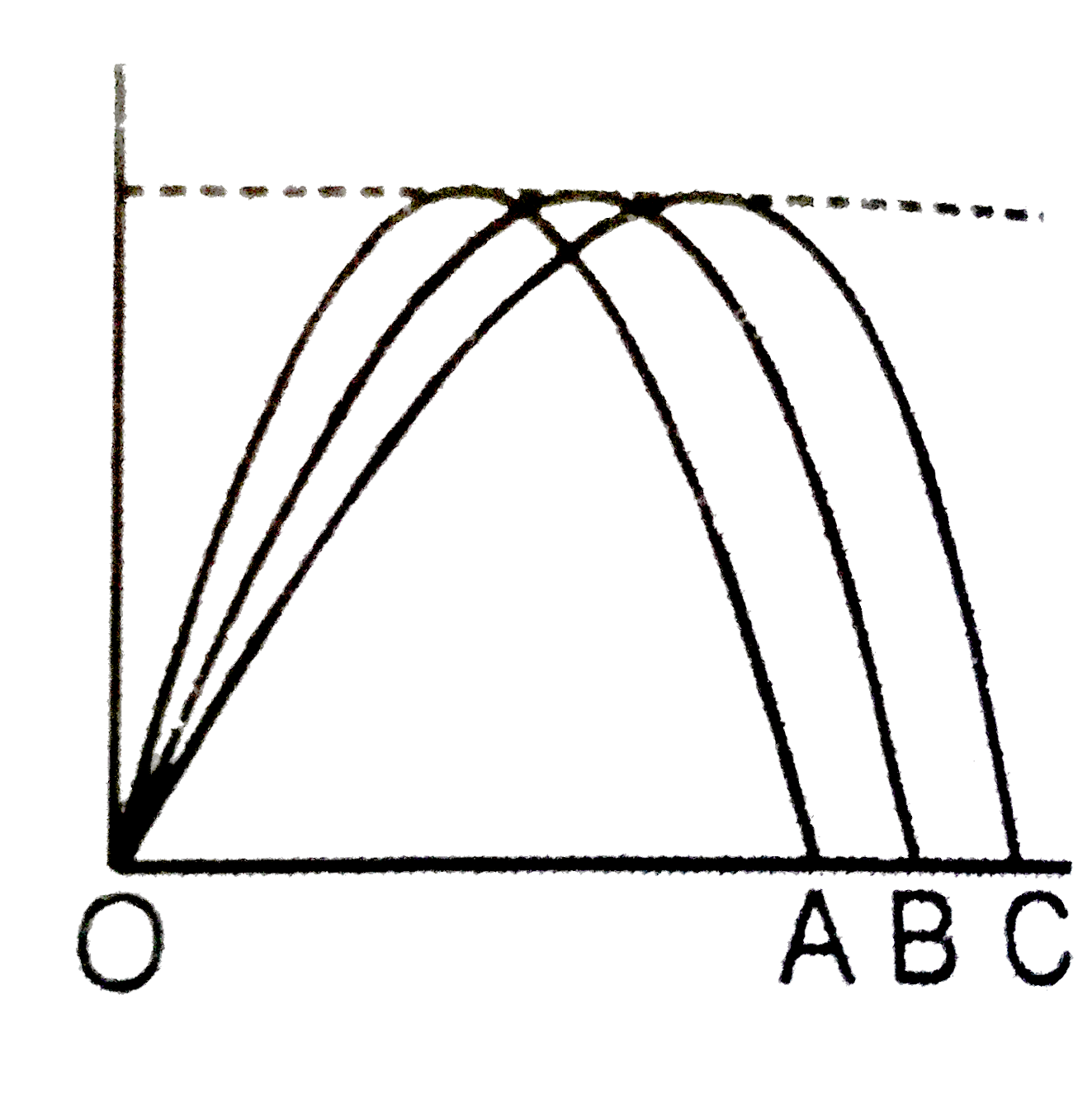
View SolutionThree projectile A, B and C are thrwon from the same point in the same plane. Their trajectories are shown in the figure. Then which of the following statement is true:-
View SolutionThree particles A, B and C are projected from the same point with the same initial speeds making angles 30∘,45∘and60∘ respectively with the horizontal. Which of the following statement is correct?
View Solution
