Infinite number of masses, each of mass 3 kg are placed along the y-axis at y = 1 m, 3 m, 9 m 27 m ... The magnitude of resultant gravitational potential in terms of gravitatinal constant at the origin (y = 0) is
4.5 G unit
6 G unit
3 G unit
9 unit
The correct Answer is:A
To solve the problem of finding the magnitude of the resultant gravitational potential at the origin due to an infinite number of masses placed along the y-axis, we can follow these steps:
Step 1: Identify the positions of the masses
The masses are located at positions y=1m,3m,9m,27m,…. These positions can be expressed as yn=3n−1 for n=1,2,3,….
Step 2: Write the formula for gravitational potential
The gravitational potential V at a point due to a mass m at a distance r is given by:
V=−Gmr
where G is the gravitational constant.
Step 3: Calculate the gravitational potential at the origin due to each mass
For each mass located at yn=3n−1, the distance from the origin (which is at y=0) is rn=3n−1. Therefore, the gravitational potential at the origin due to the mass at yn is:
Vn=−G⋅3kg3n−1=−3G3n−1=−3G⋅3−n+1
Step 4: Sum the gravitational potentials from all masses
The total gravitational potential V at the origin is the sum of the potentials due to all the masses:
V=∞∑n=1Vn=∞∑n=1−3G⋅3−n+1
This can be simplified to:
V=−3G∞∑n=13−n+1=−3G⋅3∞∑n=0(13)n
Step 5: Recognize the series as a geometric series
The series ∞∑n=0(13)n is a geometric series with first term a=1 and common ratio r=13. The sum of an infinite geometric series is given by:
S=a1−r=11−13=123=32
Step 6: Substitute the sum back into the potential equation
Substituting back into the potential equation:
V=−3G⋅3⋅32=−27G2
Step 7: Take the magnitude of the gravitational potential
The magnitude of the gravitational potential at the origin is:
|V|=27G2
Final Answer
Thus, the magnitude of the resultant gravitational potential at the origin in terms of the gravitational constant G is:
27G2
The masses are located at positions y=1m,3m,9m,27m,…. These positions can be expressed as yn=3n−1 for n=1,2,3,….
The gravitational potential V at a point due to a mass m at a distance r is given by:
V=−Gmr
where G is the gravitational constant.
For each mass located at yn=3n−1, the distance from the origin (which is at y=0) is rn=3n−1. Therefore, the gravitational potential at the origin due to the mass at yn is:
Vn=−G⋅3kg3n−1=−3G3n−1=−3G⋅3−n+1
The total gravitational potential V at the origin is the sum of the potentials due to all the masses:
V=∞∑n=1Vn=∞∑n=1−3G⋅3−n+1
This can be simplified to:
V=−3G∞∑n=13−n+1=−3G⋅3∞∑n=0(13)n
The series ∞∑n=0(13)n is a geometric series with first term a=1 and common ratio r=13. The sum of an infinite geometric series is given by:
S=a1−r=11−13=123=32
Substituting back into the potential equation:
V=−3G⋅3⋅32=−27G2
The magnitude of the gravitational potential at the origin is:
|V|=27G2
Thus, the magnitude of the resultant gravitational potential at the origin in terms of the gravitational constant G is:
27G2
Topper's Solved these Questions
Similar Questions
An infinite number of particles each of mass m are placed on the positive X-axis of 1m,2m,4m,8m,... from the origin. Find the magnitude of the resultant gravitational force on mass m kept at the origin.
View SolutionInfinite number of bodies, each of mass 2kg are situated on X-axis at distance 1m,2m,4m,8m, respectively from the origin, What is the resulting gravitational potential due to this system at the origin ?
View Solution
Knowledge Check
Infinite number of masses, each of 1kg, are placed along the x-axis at x=±1m,±2m,±4m,±8m,±16m.. The gravitational of the resultant gravitational potential in term of gravitaitonal constant G at the origin (x=0) is
AG2BGC2GD4GInfinite number of masses, each of 1kg, are placed along the x-axis at x=±1m,±2m,±4m,±8m,±16m.. The gravitational of the resultant gravitational potential in term of gravitaitonal constant G at the origin (x=0) is
AGB3GC2GD8GInfinite number of masses, each of 1kg, are placed along the x-axis at x=±1m,±2m,±4m,±8m,±16m.. The gravitational of the resultant gravitational potential in term of gravitaitonal constant G at the origin (x=0) is
AG/2BGC2GD4G
Infinite number of masses, each of 1kg, are placed along the x-axis at x=±1m,±2m,±4m,±8m,±16m.. The gravitational of the resultant gravitational potential in term of gravitaitonal constant G at the origin (x=0) is
View SolutionInfinite number of bodies, each of mass 2kg, are situated on x-axis at distance 1m,2m,4m,8m......... respectively, from the origin. The resulting gravitational potential the to this system at the origing will be
View SolutionInfinite number of charges of 4μC, respectively are placed along the X-axis at 1 m, 2 m, 4 m, 8 m and So. The coulomb field at origin for all these charges is:
View SolutionA large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
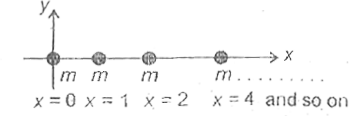
View SolutionA number of particles each of mass 0.75kg are placed at distances 1m, 2m, 4m, 8m etc. from origin along positive X axis. the intensity of gravitational field at the origin will be -
View Solution
