A battery of EMF E produces currents 4 A and 3 A when connected to external resistance and respectively. The internal resistance of the battery is
The correct Answer is:B
To find the internal resistance of the battery given the currents produced by different external resistances, we can follow these steps:
Step 1: Understand the Problem
We have a battery with an EMF E that produces currents of 4 A and 3 A when connected to external resistances of 1 Ω and 2 Ω, respectively. We need to find the internal resistance r of the battery.
Step 2: Set Up the Equations
Using Ohm's law, we can express the EMF in terms of the current and resistances.
1. When connected to 1 Ω:
E=I1⋅(R+r)=4⋅(1+r)
This gives us our first equation:
E=4(1+r)(Equation 1)
2. When connected to 2 Ω:
E=I2⋅(R+r)=3⋅(2+r)
This gives us our second equation:
E=3(2+r)(Equation 2)
Step 3: Equate the Two Expressions for EMF
Since both equations represent the same EMF E, we can set them equal to each other:
4(1+r)=3(2+r)
Step 4: Solve for r
Expanding both sides:
4+4r=6+3r
Now, rearranging the equation to isolate r:
4r−3r=6−4
r=2Ω
Conclusion
The internal resistance of the battery is 2Ω.
---
We have a battery with an EMF E that produces currents of 4 A and 3 A when connected to external resistances of 1 Ω and 2 Ω, respectively. We need to find the internal resistance r of the battery.
Using Ohm's law, we can express the EMF in terms of the current and resistances.
E=I1⋅(R+r)=4⋅(1+r)
This gives us our first equation:
E=4(1+r)(Equation 1)
E=I2⋅(R+r)=3⋅(2+r)
This gives us our second equation:
E=3(2+r)(Equation 2)
Since both equations represent the same EMF E, we can set them equal to each other:
4(1+r)=3(2+r)
Expanding both sides:
4+4r=6+3r
Now, rearranging the equation to isolate r:
4r−3r=6−4
r=2Ω
The internal resistance of the battery is 2Ω.
Topper's Solved these Questions
Similar Questions
A battery of emf ε and internal resistance r sends currents I1 and I2, when connected to external resistance R1 and R2 respectively. Find the emf and internal resistance of the battery.
View SolutionA battery supplies 150W and 196 W power to two resistance of 6Ω and 4Ω when they are connected separately to it. The internal resistance of the battery is:-
View Solution
Knowledge Check
A current of 2 A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5 A when connected across a 9 Ω resistor. The internal resistance of the battery is
A1ΩB2ΩC13ΩD14ΩA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
A1/3ΩB1/4ΩC1ΩD0.5ΩA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor The internal resistance of the battery is
A13ΩB14ΩC5ΩD0.5Ω
A battery of emf ε and internal resistance r, when connected across an external resistance of 12 Ω , produces a current of 0.5 A. When connected across a resistance of 25Ω, it produces a current of 0.25 A. Determine the emf and internal resistance of the cell.
View SolutionA galvanometer, together with an unknown resistance in series, is connected across two identical batteries of each 1.5V. When the batteries are connected in series,the galvanometer records a current of 1A, and when the batteries are connected in parallel, the current is 0.6A. In this case, the internal resistance of the battery is 1/'∗'Ω.
What is the value of '**'?
View SolutionThree cells of emf 2.0 v, 1.8 V and 1.5 V are connected in series. Their internal resistances are 0.05Ω,0.7Ω and 1Ω respectively. If the battery is connected to an external resistor of 4Ω via a very resistance ammeter, what would be the reading in the ammeter ?
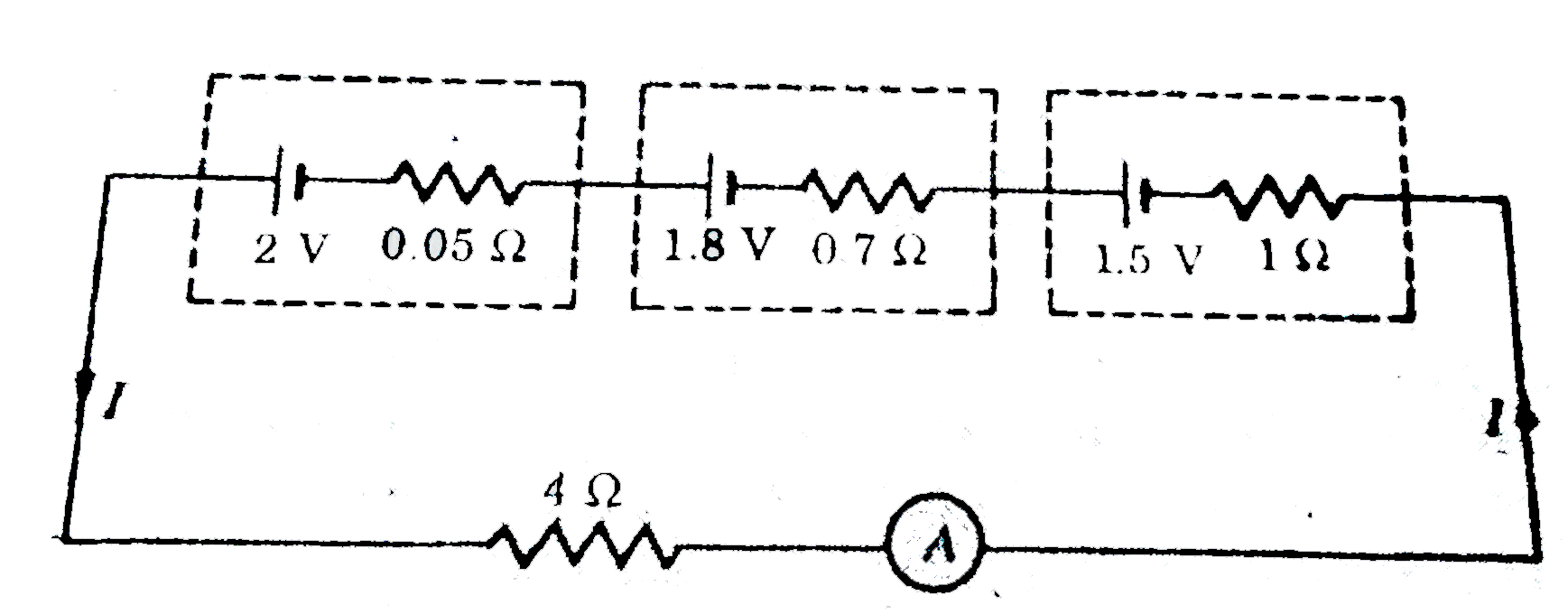
View SolutionTwo batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
View SolutionWhen a battery connected across a resistor of 16Ω, the voltage across the resistor is 12 V. When the same battery is connected across a resistor of 10Ω, voltage across it is 11 V. The internal resistance of the battery (in ohm) is
View Solution