At a place horizontal and vertical components of BH=312G, 50West of North. Bv=1G vetically upward. Then angle of inclination and declination are respectively earth's magnetic field are as follows
600, 50 W
30,50 W
300, 50 E
600, 50 E
The correct Answer is:B
To solve the problem, we need to determine the angle of inclination and declination of the Earth's magnetic field based on the given horizontal and vertical components of the magnetic field.
Given:
- Horizontal component of the magnetic field, BH=31/2G at an angle of 5∘ West of North.
- Vertical component of the magnetic field, BV=1G vertically upward.
Step 1: Understanding the Components
The horizontal component BH is directed at 5∘ West of North. This means that the magnetic field is tilted towards the west from the north direction.
Step 2: Calculate the Angle of Inclination
The angle of inclination θ can be calculated using the formula:
tan(θ)=BVBH
Substituting the values:
tan(θ)=1G31/2G=1√3
From trigonometric values, we know that:
tan(30∘)=1√3
Thus, we find:
θ=30∘
Step 3: Determine the Angle of Declination
The declination angle D is the angle between the magnetic meridian and the geographic meridian. Since the horizontal component is directed 5∘ West of North, the declination angle is:
D=5∘West
Conclusion
The angles of inclination and declination are:
- Angle of Inclination θ=30∘
- Angle of Declination D=5∘West
Final Answer
The angle of inclination and declination are respectively 30∘ and 5∘West.
---
- Horizontal component of the magnetic field, BH=31/2G at an angle of 5∘ West of North.
- Vertical component of the magnetic field, BV=1G vertically upward.
The horizontal component BH is directed at 5∘ West of North. This means that the magnetic field is tilted towards the west from the north direction.
The angle of inclination θ can be calculated using the formula:
tan(θ)=BVBH
Substituting the values:
tan(θ)=1G31/2G=1√3
From trigonometric values, we know that:
tan(30∘)=1√3
Thus, we find:
θ=30∘
The declination angle D is the angle between the magnetic meridian and the geographic meridian. Since the horizontal component is directed 5∘ West of North, the declination angle is:
D=5∘West
The angles of inclination and declination are:
- Angle of Inclination θ=30∘
- Angle of Declination D=5∘West
The angle of inclination and declination are respectively 30∘ and 5∘West.
Topper's Solved these Questions
Similar Questions
At a particular place, horizontal and vertical components of earth's magnetic field are equal. The angle of dip at that place is…………… .
View SolutionThe horizontal and veritical components of eaths's field at a place ar 0.22 gauss of 0.38 gauss, respectively. Calculate the angle of dip and resultant intensity of earth's field.
View Solution
Knowledge Check
At a place horizontal and vertical components of BH=312G, 50West of North. Bv=1G vetically upward. Then angle of inclination and declination are respectively earth's magnetic field are as follows
A600, 50 WB30,50 WC300, 50 ED600, 50 EAt a place horizontal and vertical components of earthsmag≠ticfieldareasfollows<br>BH=1G 5^⋅ East of north
BV=1G vertically upward
Then inclination and declination are respectivelyA45∘,5∘WB5∘,45∘EC45∘,5∘ED5∘,45∘WAt a place, if the earth's horizontal and vertical components of magnetic field are equal, then the angle og dip will be
A0∘10∘WB45∘,10∘EC45∘,10∘WD10∘W,45∘
Horizontal and vertical components of earth’s magnetic field at a place are equal. The angle of dip at that place is ________.
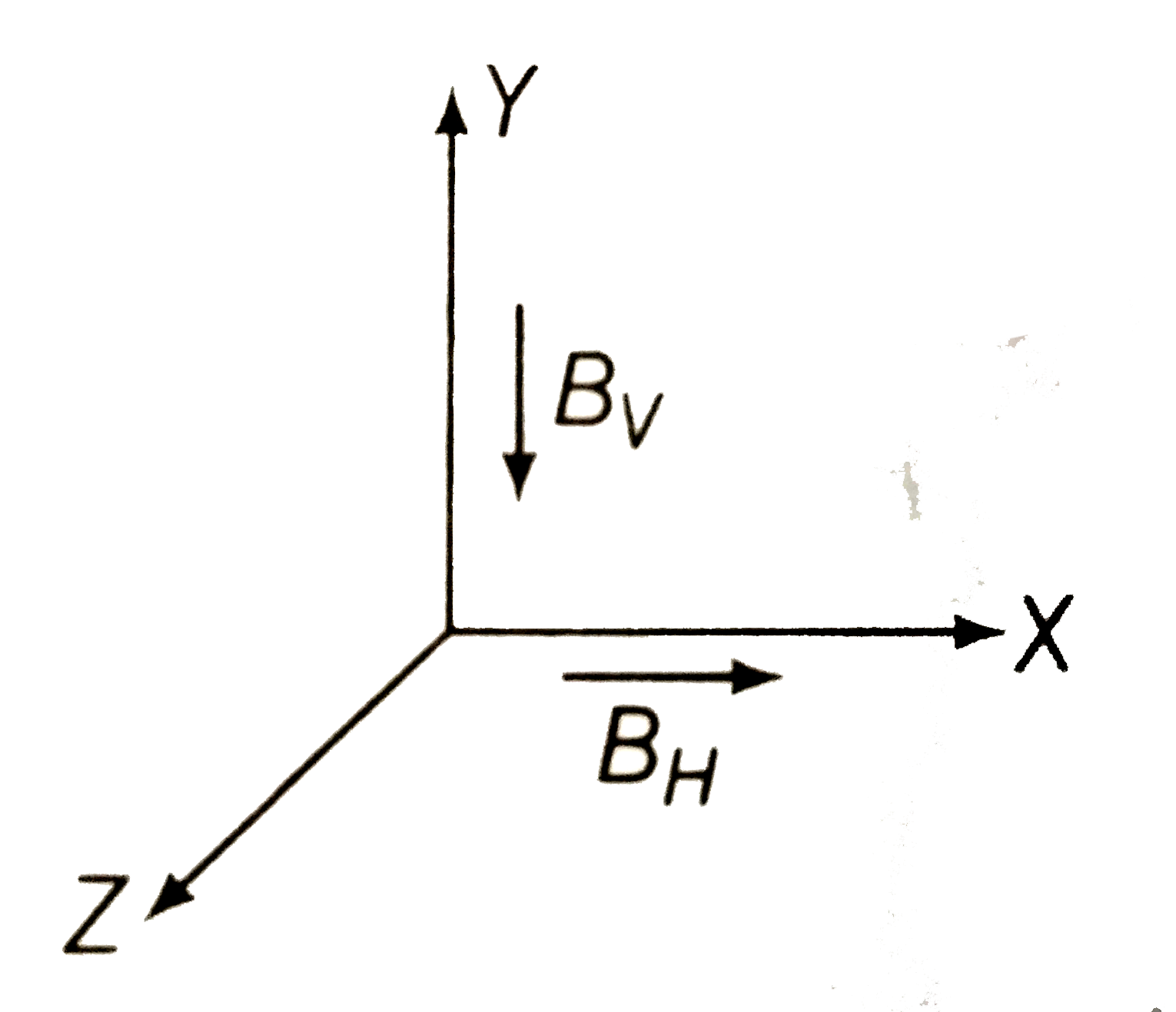
View SolutionAt a given place horizontal and vertical components of the earth's magnetic field BHandBV are along X and Y-axes, respectively, as shown in the figure. What is the total flux of the earth's magnetic field associated with an area S, if the area S is in the
(i) XY-plane
(ii) YZ-plane
View SolutionWhat is the angle of dip at a place, where the horizontal and vertical components of the earth's magnetic field are equal ?
View SolutionAt a place, horizontal and vertical components of earth's magnetic field are equal. Angle of dip at the given place is
View SolutionThe angle of dip at a certain place where the horizontal and vertical components of the earth's magnetic field are equal is
View Solution
