A cube is given and it has -q charge in one corner and +q charges in all the remaining 7 corners. Find the electric field at the center of the cube
To find the electric field at the center of a cube with a -q charge at one corner and +q charges at the other seven corners, we can follow these steps:
Step 1: Understand the Configuration
We have a cube with charges at its corners. One corner has a charge of -q, and the other seven corners each have a charge of +q. The goal is to find the electric field at the center of the cube.
Step 2: Identify the Electric Field Contribution
The electric field at a point due to a point charge is given by the formula:
E=k|q|r2
where E is the electric field, k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the electric field is being calculated.
Step 3: Calculate the Distance to the Center
The distance from each corner of the cube to the center can be determined using the geometry of the cube. The length of the diagonal of the cube is given by:
d=a√3
where a is the side length of the cube. Therefore, the distance from each corner to the center of the cube is:
r=d2=a√32
Step 4: Calculate the Electric Field Contributions
1. From the -q Charge:
The electric field due to the -q charge at the center will point towards the -q charge (since electric field lines point towards negative charges). The magnitude is:
E−q=kq(a√32)2=4kq3a2
2. From Each +q Charge:
Each +q charge will produce an electric field pointing away from itself. The contribution from each +q charge is:
E+q=kq(a√32)2=4kq3a2
Since there are 7 +q charges, the total contribution from all +q charges is:
E+q,total=7⋅4kq3a2=28kq3a2
Step 5: Determine the Net Electric Field
The net electric field at the center of the cube is the vector sum of the electric fields due to the -q charge and the total contribution from the +q charges. The direction of the electric field due to the -q charge is towards it, while the direction of the electric fields due to the +q charges is away from them. Therefore, we can express the net electric field as:
Enet=E+q,total−E−q=28kq3a2−4kq3a2=24kq3a2=8kqa2
Step 6: Direction of the Electric Field
The direction of the net electric field will be away from the center towards the direction of the majority of the positive charges, which is the direction opposite to the -q charge.
Final Answer
The electric field at the center of the cube is:
E=8kqa2
and it points away from the -q charge.
We have a cube with charges at its corners. One corner has a charge of -q, and the other seven corners each have a charge of +q. The goal is to find the electric field at the center of the cube.
The electric field at a point due to a point charge is given by the formula:
E=k|q|r2
where E is the electric field, k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the electric field is being calculated.
The distance from each corner of the cube to the center can be determined using the geometry of the cube. The length of the diagonal of the cube is given by:
d=a√3
where a is the side length of the cube. Therefore, the distance from each corner to the center of the cube is:
r=d2=a√32
1. From the -q Charge:
The electric field due to the -q charge at the center will point towards the -q charge (since electric field lines point towards negative charges). The magnitude is:
E−q=kq(a√32)2=4kq3a2
Each +q charge will produce an electric field pointing away from itself. The contribution from each +q charge is:
E+q=kq(a√32)2=4kq3a2
Since there are 7 +q charges, the total contribution from all +q charges is:
E+q,total=7⋅4kq3a2=28kq3a2
The net electric field at the center of the cube is the vector sum of the electric fields due to the -q charge and the total contribution from the +q charges. The direction of the electric field due to the -q charge is towards it, while the direction of the electric fields due to the +q charges is away from them. Therefore, we can express the net electric field as:
Enet=E+q,total−E−q=28kq3a2−4kq3a2=24kq3a2=8kqa2
The direction of the net electric field will be away from the center towards the direction of the majority of the positive charges, which is the direction opposite to the -q charge.
The electric field at the center of the cube is:
E=8kqa2
and it points away from the -q charge.
Similar Questions
A positive charge q is placed in front of cinducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube due to the charges appearing on its surface.
View SolutionEight identical point charges of q coulomb each are placed at the corners of a cube side 0.1m. Calculate electric field at the centre of the cube. Calculate the field at the center when one of the corner charges is removed.
View Solution
Knowledge Check
A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :
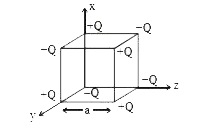 A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)A charge +q is placed at a distance 'd' from the centre of the uncharged metallic cube of side 'a'. The electric field at the centre of the cube due to induced charges on the cube will be
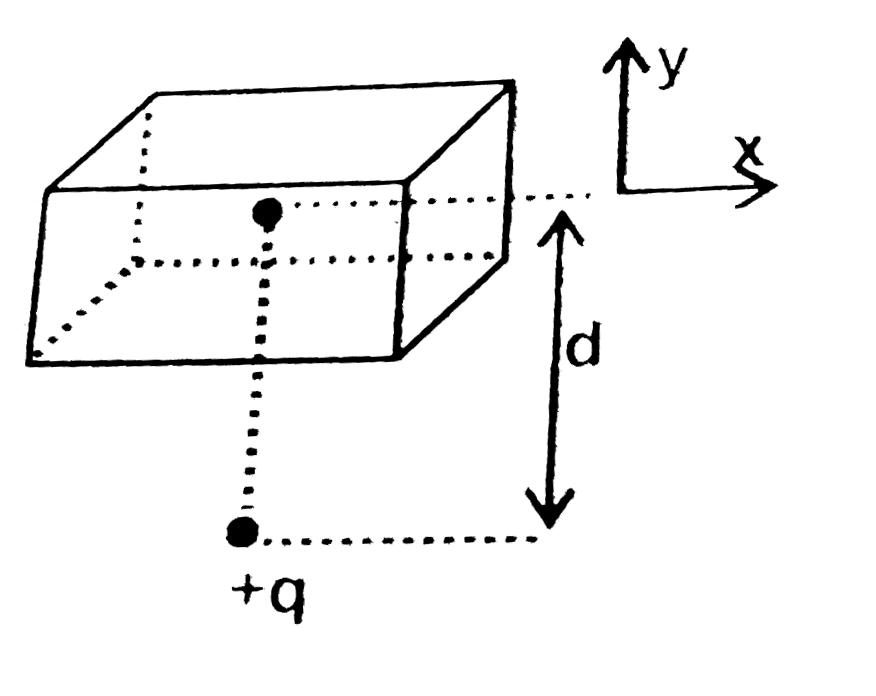 AzeroBq4π∈0d2(−ˆj)Cq4π∈0d2(ˆj)Dq4π∈0(d−a2)(−ˆj)
AzeroBq4π∈0d2(−ˆj)Cq4π∈0d2(ˆj)Dq4π∈0(d−a2)(−ˆj)Three equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
Akq/r2B3kq/r2C√3kq/r2Dzero
A charge Q is placed at the centre of a cub. Find the flux of the electric field through the six surfaced of the cube.
View SolutionA cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionA charge 'Q' is placed at each corner of a cube of side 'a'. The potential at the centre of the cube is
View Solution
