Find the minimum force F0 that should be applied to the block of mass m = 0.5 kg so that the block stays in equilibrium with the rough vertical wall having friction coefficient μ=0.2 (Take g=10ms2)
25N
20N
50N
None of these
To find the minimum force F0 that should be applied to a block of mass m=0.5kg so that it stays in equilibrium against a rough vertical wall with a friction coefficient μ=0.2, we can follow these steps:
Step 1: Calculate the Weight of the Block
The weight W of the block can be calculated using the formula:
W=m⋅g
where g=10m/s2 (acceleration due to gravity).
Substituting the values:
W=0.5kg⋅10m/s2=5N
Step 2: Set Up the Forces Acting on the Block
In equilibrium, the forces acting on the block must balance. The forces acting on the block are:
- The weight W acting downwards.
- The frictional force Fs acting upwards.
- The normal force N acting horizontally from the wall.
Step 3: Relate the Frictional Force to the Normal Force
The maximum frictional force Fs can be expressed as:
Fs=μ⋅N
where μ=0.2 is the coefficient of friction.
Step 4: Apply the Equilibrium Condition in the Vertical Direction
For the block to be in equilibrium in the vertical direction, the upward frictional force must balance the downward weight:
Fs=W
Substituting the expression for Fs:
μ⋅N=W
Step 5: Substitute for Normal Force N
From the equilibrium condition in the horizontal direction, we know that:
N=F0
Thus, we can rewrite the equation as:
μ⋅F0=W
Step 6: Solve for F0
Rearranging the equation gives:
F0=Wμ
Substituting the values we have:
F0=5N0.2=25N
Conclusion
The minimum force F0 that should be applied to the block to keep it in equilibrium is:
F0=25N
The weight W of the block can be calculated using the formula:
W=m⋅g
where g=10m/s2 (acceleration due to gravity).
W=0.5kg⋅10m/s2=5N
In equilibrium, the forces acting on the block must balance. The forces acting on the block are:
- The weight W acting downwards.
- The frictional force Fs acting upwards.
- The normal force N acting horizontally from the wall.
The maximum frictional force Fs can be expressed as:
Fs=μ⋅N
where μ=0.2 is the coefficient of friction.
For the block to be in equilibrium in the vertical direction, the upward frictional force must balance the downward weight:
Fs=W
Substituting the expression for Fs:
μ⋅N=W
From the equilibrium condition in the horizontal direction, we know that:
N=F0
Thus, we can rewrite the equation as:
μ⋅F0=W
Rearranging the equation gives:
F0=Wμ
Substituting the values we have:
F0=5N0.2=25N
The minimum force F0 that should be applied to the block to keep it in equilibrium is:
F0=25N
Similar Questions
Find the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View SolutionA body of mass 10 kg is pulled with a time varying horizontal force F=2t2 N on a rough surface having friction coefficient μ=0.2. Find the speed of block after 6 seconds.
View Solution
Knowledge Check
A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When
 AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.
AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.A board of mass m = 1 kg lies on a table and a weight of M = 2 kg on the board. What minimum force F must be applied on the board in order to pull it out from under the road ? The coefficient of friction between board and table is μ2=0.5 : (Take g=10m/s2)
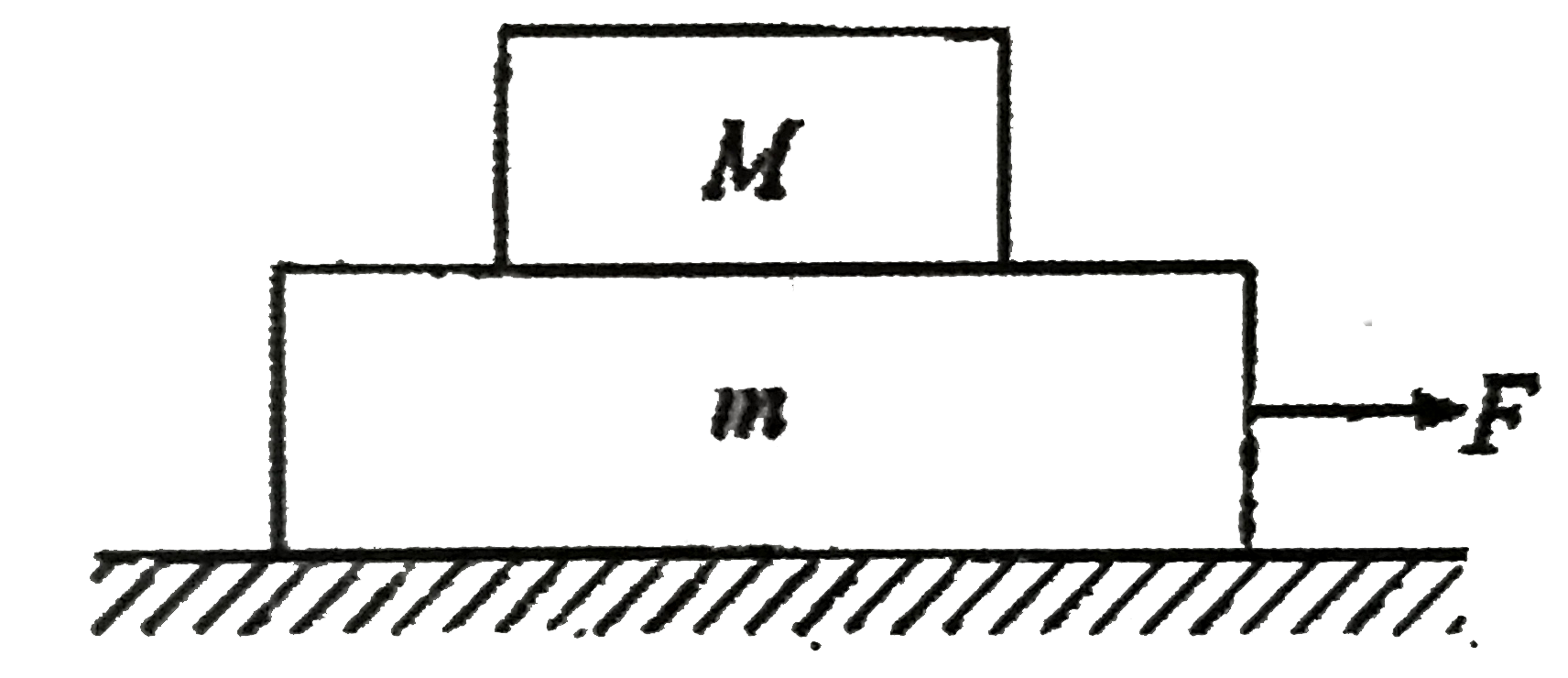 A7.5 NB15 NC22.5 ND30 N
A7.5 NB15 NC22.5 ND30 NA rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30∘ with the horizontal plane , what is the force of friction on the block ? (Take g = 10m/s2)
A5 NB10 NC12 ND20 N
A force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA block of mass 10 kg is released on rough incline plane. Block start descending with acceleration 2m/s2. Kinetic friction force acting on block is (take g=10m/s2)
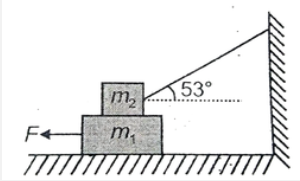
View SolutionCalculate the Force (F) required to cause the block of mass m1=20kg just to slide under the block of mass m2=10kg [ coefficient of friction μ=0⋅25 for all surfaces ]
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionA force of 100N is applied on a block of mass 3 kg as shown in the figure-2.164. The coefficient of friction between the surface and the block is 0.25.The frictional force acting on the block is: (Take g=10ms2)
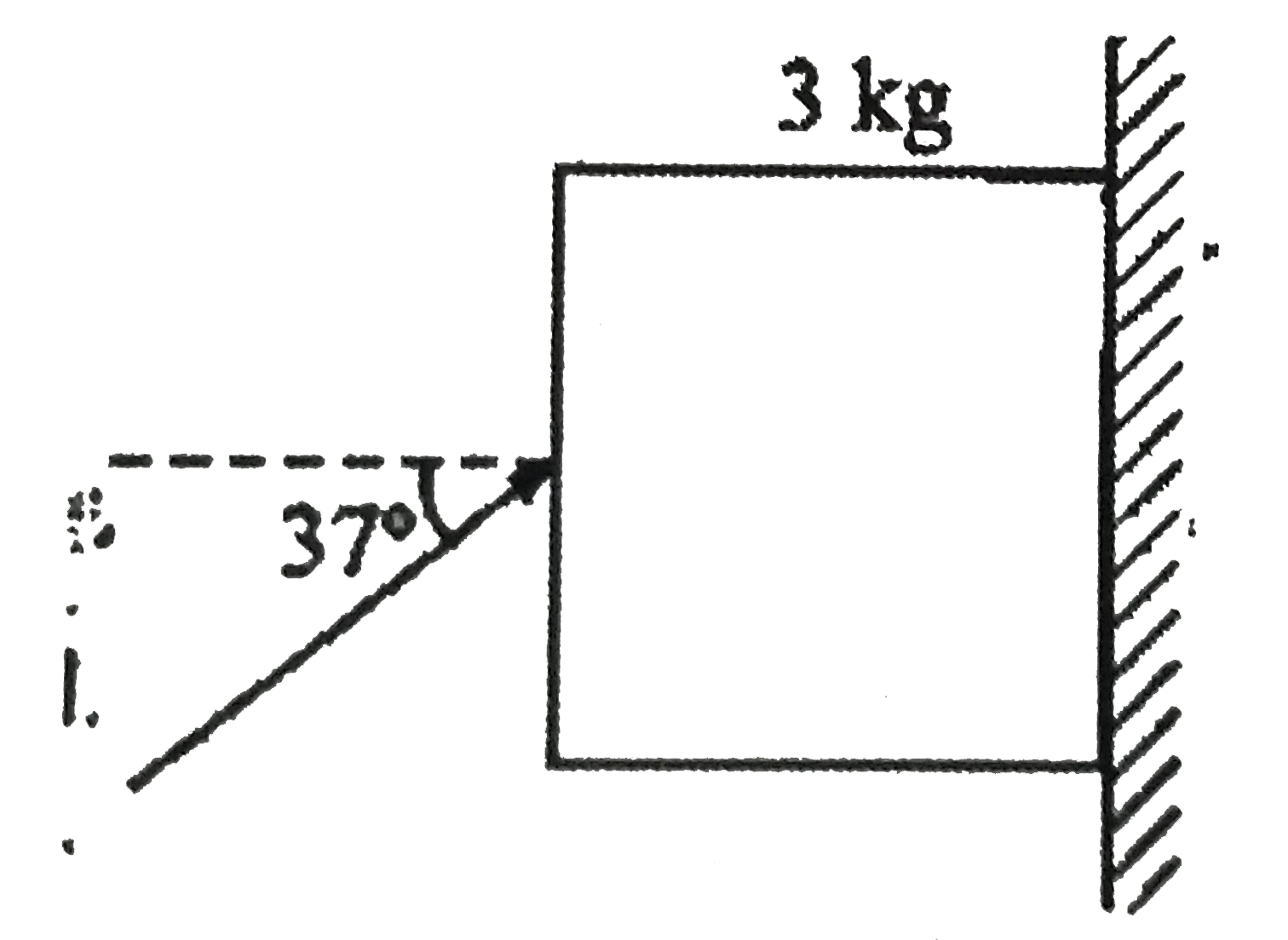
View Solution
