(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Fig. 6.06.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s. Calculate the induced emf in the loop at the instant when x = 0.2 m. Take a = 0.1 m and assume that the loop has a large resistance.
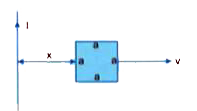
(a) The magnetic field due to straight wire has magnitude B1=(μ0I)2πr, at a distance r from the wire and according to right hand rule B1 points directly into the page within the loop.
The magnetic flux ϕ2 linking the loop is
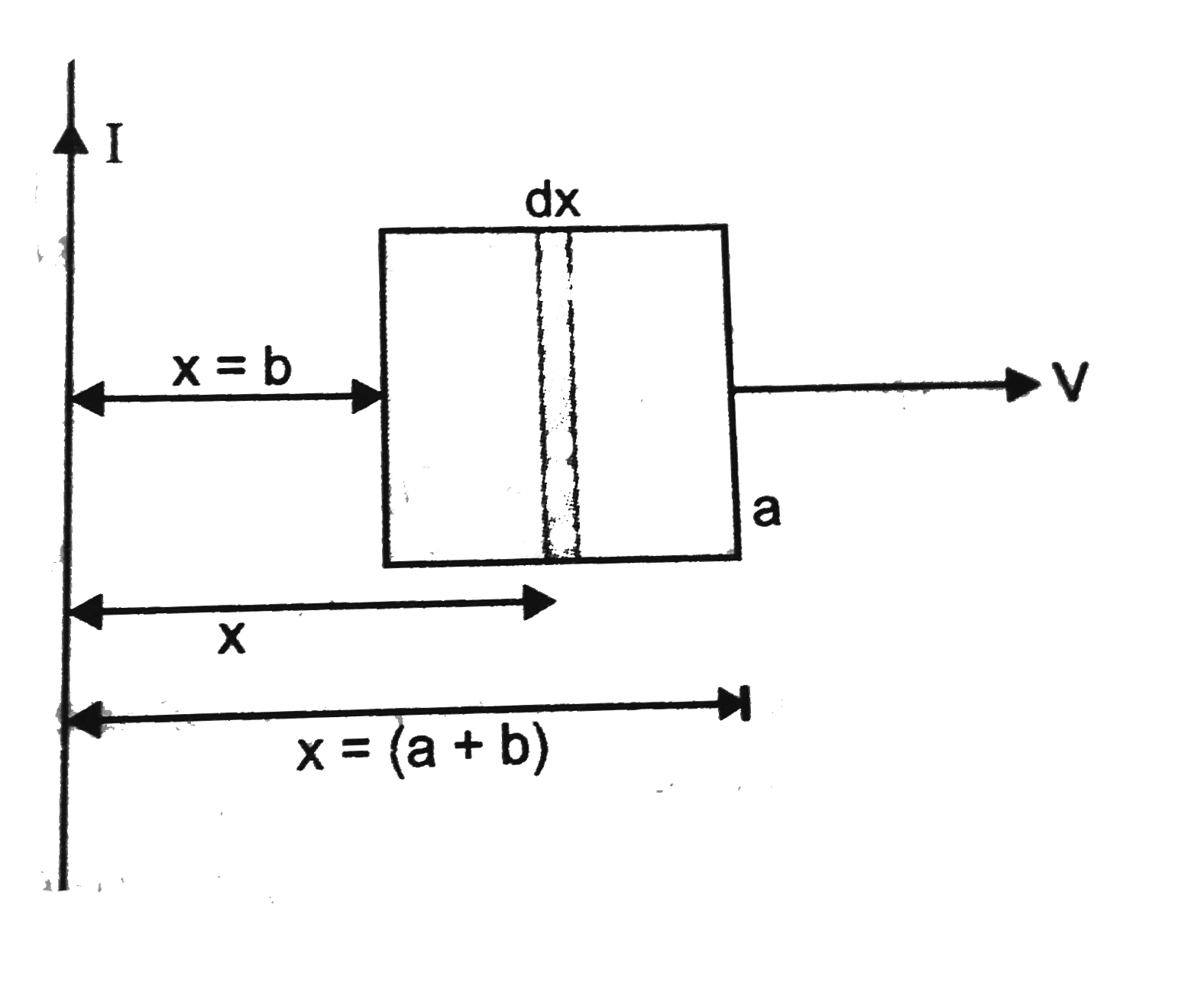
ϕ12=∫vceB1.dvceA2, where dA2 is the area of an elementary strip as shown in Fig. 6.07 having a value dA2=adr and r ranges from rmin=r→rmax=(x+a).
Therefore, ϕ12=∫x+ax(μ0I2πr).adr=μ0Ia2π∫x+zxdrr
=μ0Ia2πIn(x+ax)=μ0a2πIn(1+ax)
Therefore, the mutual inductance
M=M12=ϕ12I=μ0a2πIn(1+ax)
(b) The square loop is moving in a non uniform magnetic field. The magnetic flux linked with the loop at any instant is
ϕB=μ0Ia2πIn(1+ax)
∴ Induced emf ɛ=−dϕBdt=−dϕBdx.0dxdt=−vdϕBdx=−ddx[μ0Ia2π.In(1+ax)]
=−vμ0Ia2π.(−a/x2)(1+xa)μ02π.a2vx(x+4).I
In the present problem a=0.1m,x=0.2m,v=10ms−1,I=50A
∴∣∣ɛ∣∣=4π×10−72π.(0.1)2(10)(0.2)(0.2+0.1)×50=1.7×10−5V.
Topper's Solved these Questions
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Case Based/Source-Based Integrated Questions
3 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Multiple Choice Questions
30 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- ELECTROMAGNETIC WAVESBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SELF ASSESSMENT TEST (SECTION C)
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
Similar Questions
Find the mutual inductance between the straight wire and the square loop of figure.
View Solution(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Fig.
(b) Evaluate the induced emf in loop if the wire carries a current of 50 A and the loop has an instantaneous velocity υ=10ms−1 at the location x = 0.2 m, as shown. Take a = 0.1m and assume that the loop has a large resistance.
View Solution
Knowledge Check
The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
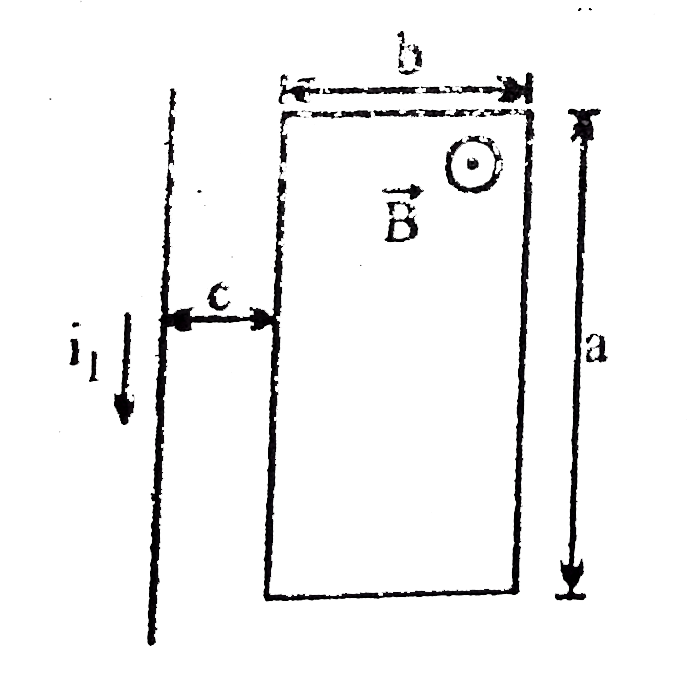 AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc)
AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc)The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
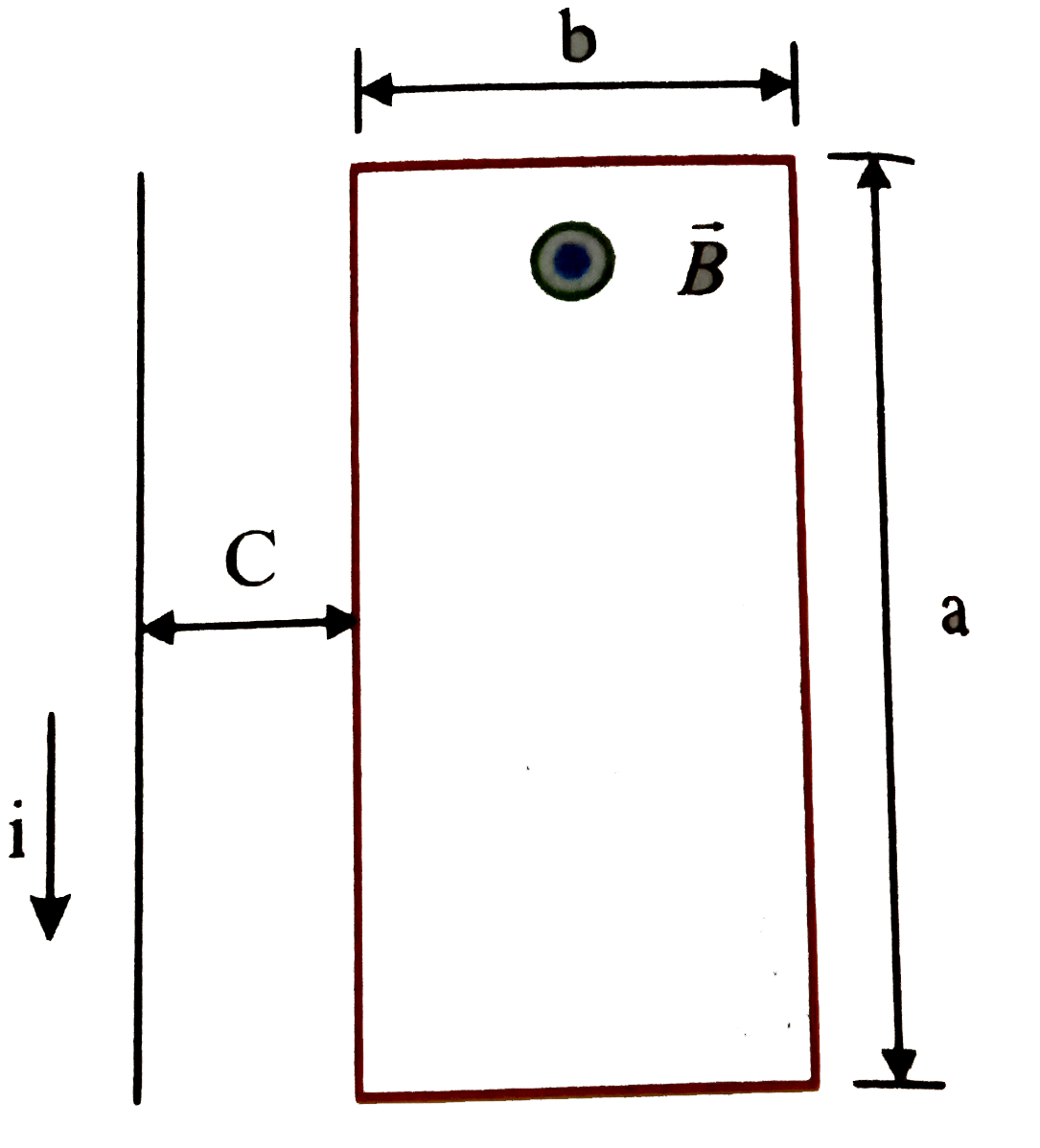 AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb)
AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb)
Find the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.

View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.

View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
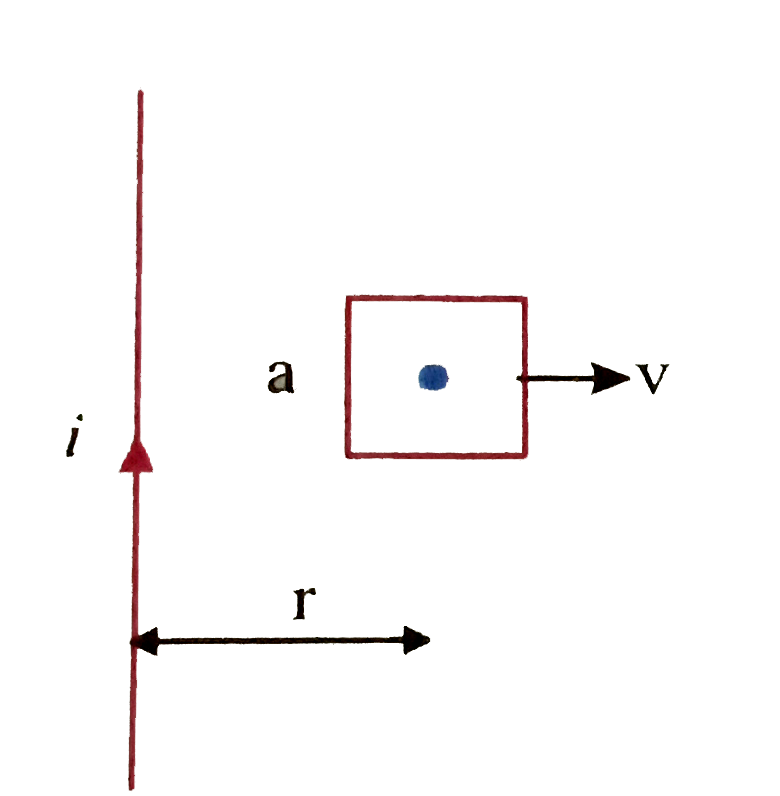
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is

View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
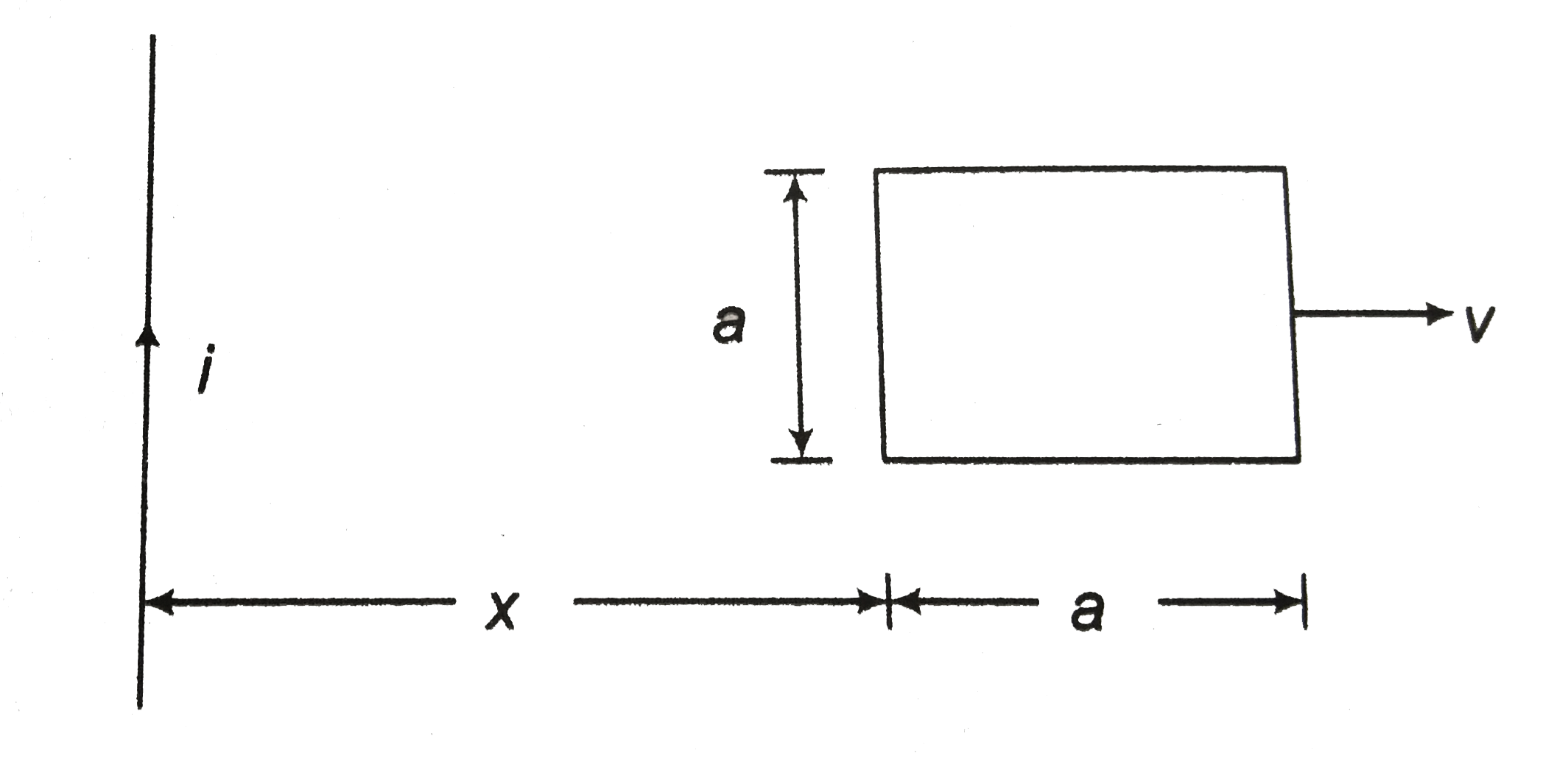
View Solution
