Find the equation of the tangent at the
point 30∘ (parametric value of θ) of the
circle is x2+y2+4x+6y−39=0.Solution in Telugu
The correct Answer is:√3x+y+3+2(√3−2√13)=0
Step by step video, text & image solution for Find the equation of the tangent at the point 30^(@) (parametric value of theta) of the circle is x^(2) + y^(2) + 4x +6y - 39=0. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CIRCLEEXERCISE - EXERCISE -1.355videos
CIRCLE
- BOOK - AAKASH SERIESCHAPTER - CIRCLEEXERCISE - EXERCISE -1.438videos
CIRCLE
- BOOK - AAKASH SERIESCHAPTER - CIRCLEEXERCISE - EXERCISE -1.1108videos
CIRCLE
- BOOK - AAKASH SERIESCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE - 1.4 (Level-2)36videos
BINOMIAL THEOREM
- BOOK - AAKASH SERIESCHAPTER - CIRCLESEXERCISE - PRACTICE EXERCISE164videos
CIRCLES
Similar Questions
Find the chord of contact of (1,1) to the
circle x2+y2=9.03:48View SolutionDiscuss the relative position of the fol-
lowing pair of circles.
x2+y2−4x−6y−12=0
x2+y2+6x+18y+26=0.11:24View SolutionFind the equation of the circle with centre
C and redius r where.
C=(a,−b),r=a+b02:08View SolutionFind the coefficient of term independent of x in the expansion of (x+1x2/3−x1/3+1−x−1x−x1/2)10
07:53View SolutionThe circle with centre (1,1) and radius 1 is
02:54View SolutionTangents are drawn from a point on the circle x2+y2−4x+6y−37=0 to the circle x2+y2−4x+6y−12=0. The angle between the tangents, is
02:26View SolutionFind the equation of the tangent at the
point 30∘ (parametric value of θ) of the
circle is x2+y2+4x+6y−39=0.04:22View SolutionObtain the parametric equation of each
of the following circles.
x2+y2−4x−6y−12=004:27View SolutionFind the equations of the tangents from the point A(3,2) to the circle x2+y2+4x+6y+8=0.
07:57View SolutionThe parametric equation of the circle x2+y2+8x−6y=0 are
04:05View SolutionFind the equation of the tangent at the specified points to each of the following curves.
the circle x2+y2−4x−6y−3=0at(2,−1)02:54View SolutionFind the length of the tangent from any point on the circule
x2+y2−4x+6y−2=0 to the circle x2+y2−4x+6y+7=004:48View Solutionস্পর্শকের দৈর্ঘ্য নির্ণয় করো:
x2+y2−4x+6y−2=0 বৃত্তের ওপর যে-কোনো বিন্দু থেকে x2+y2−4x+6y+7=0 বৃত্তে অঙ্কিত স্পর্শকের দৈর্ঘ্য নির্ণয় করো06:07View SolutionIf x+y+7=0 is a tangent to the circle x2+y2−4x−6y+k=0 then the point of contact is
04:29View SolutionFind the point of intersection of the circle x2+y2+4x+6y−39=0 and the normal at (2,3).
08:14View SolutionFind the length of a tangent drawn from the point (3,4) to the circle x2+y2−4x+6y−3=0.
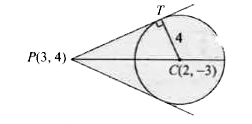03:27View Solution