An object is moving with speed v and collides with an identical mass at rest. After collision they both move at angle 30∘ with original direction. Find ratio of final speed of the mass to initial speed.
12
2
√3
1√3
To solve the problem of an object colliding with an identical mass at rest and both moving at an angle of 30 degrees after the collision, we will use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
- An object of mass m is moving with speed v in the positive x-direction.
- An identical mass m is at rest.
Step 2: Define the Final Velocities
- After the collision, both masses move at an angle of 30∘ with respect to the original direction (the x-axis).
- Let V1 be the final speed of the first mass after the collision.
- Let V2 be the final speed of the second mass after the collision.
Step 3: Apply Conservation of Momentum in the Y-Direction
- The initial momentum in the y-direction is zero because both masses are initially moving along the x-axis.
- After the collision, the momentum in the y-direction can be expressed as:
mV1sin(30∘)−mV2sin(30∘)=0
- This simplifies to:
V1sin(30∘)=V2sin(30∘)
- Since sin(30∘)=12, we can cancel it out:
V1=V2
Step 4: Apply Conservation of Momentum in the X-Direction
- The initial momentum in the x-direction is mv.
- After the collision, the momentum in the x-direction is:
mV1cos(30∘)+mV2cos(30∘)=mv
- Since V1=V2, we can substitute V2 with V1:
2mV1cos(30∘)=mv
- Dividing by m gives:
2V1cos(30∘)=v
Step 5: Solve for V1
- We know cos(30∘)=√32:
2V1(√32)=v
- This simplifies to:
V1√3=v
- Thus:
V1=v√3
Step 6: Find the Ratio of Final Speed to Initial Speed
- The ratio of the final speed V1 to the initial speed v is:
V1v=v/√3v=1√3
Final Answer
The ratio of the final speed of the mass to the initial speed is:
1√3
---
- An object of mass m is moving with speed v in the positive x-direction.
- An identical mass m is at rest.
- After the collision, both masses move at an angle of 30∘ with respect to the original direction (the x-axis).
- Let V1 be the final speed of the first mass after the collision.
- Let V2 be the final speed of the second mass after the collision.
- The initial momentum in the y-direction is zero because both masses are initially moving along the x-axis.
- After the collision, the momentum in the y-direction can be expressed as:
mV1sin(30∘)−mV2sin(30∘)=0
- This simplifies to:
V1sin(30∘)=V2sin(30∘)
- Since sin(30∘)=12, we can cancel it out:
V1=V2
- The initial momentum in the x-direction is mv.
- After the collision, the momentum in the x-direction is:
mV1cos(30∘)+mV2cos(30∘)=mv
- Since V1=V2, we can substitute V2 with V1:
2mV1cos(30∘)=mv
- Dividing by m gives:
2V1cos(30∘)=v
- We know cos(30∘)=√32:
2V1(√32)=v
- This simplifies to:
V1√3=v
- Thus:
V1=v√3
- The ratio of the final speed V1 to the initial speed v is:
V1v=v/√3v=1√3
The ratio of the final speed of the mass to the initial speed is:
1√3
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A ball moving with a velocity 12m/s strikes an identical ball at rest.After collision both balls move in directions making 300 with original direction of motion.speeds of the balls after collision are (in ms−1) ?
View SolutionA ball moving with a speed of 9ms−1 strikes an identical ball such that after the collision the direction of each ball makes and angle 30∘ with the original line of motion. Find the speeds of the two balls after the collision.
View Solution
Knowledge Check
A ball moving with velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of 30∘ with the original line of motion. What are the speeds of the balls after the collision ?
A√32msecB3msecC2√3msecD√3msecOn a friction surface a block a mass M moving at speed v collides elastic with another block of same mass M which is initially at rest . After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block's speed after the collision is
A√32vB2√23vC34vD3√2vA mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision :
AvB√3vC2√3 vDv√3
A ball moving with a speed of 9m/s strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of 30∘ with the original line of motion. Find the speeds of the two balls after collision.
View SolutionOn a frictionless surface,a block of mass M moving at speed v collides elastically with another block of same mass M which is initially at rest.After collision the first block moves at an angle θ to its initial direction and has a speed v3 .The second block's speed after the collision is ?
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v√3 in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2nd mass after collision
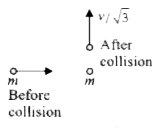
View SolutionA ball moving with a speed of 10 m s−1 strikes an identical ball such that after the collision the direction of each ball makes an angle 45∘ with the original line of motion. Find the speeds of the two balls after the collision.
View SolutionOn a frictionless surface, a block of mass M moving at speed v collides elastically with another block of same mass M which is initially at rest. After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block.s speed after the collision is
View Solution
