A wire has an elongation of 0.04m when a force F is applied on it . Now its length & diameter are double and same force F is applied on it. Find new elongation in the wire
0.06 m
0.04 m
0.02 m
0.01 m
To solve the problem, we will use the concept of stress, strain, and Young's modulus. Let's break it down step by step.
Step 1: Understand the initial conditions
We have a wire with an elongation (ΔL) of 0.04 m when a force (F) is applied to it. We denote the original length of the wire as L and its diameter as D.
Step 2: Write the formula for elongation
According to Hooke's Law, the elongation (ΔL) of a wire can be expressed as:
ΔL=F⋅LY⋅A
where:
- F is the applied force,
- L is the original length of the wire,
- Y is the Young's modulus of the material,
- A is the cross-sectional area of the wire.
The cross-sectional area A of the wire is given by:
A=πD24
Step 3: Substitute the area into the elongation formula
Substituting the area into the elongation formula, we have:
ΔL=F⋅LY⋅(πD24)=4F⋅LY⋅πD2
Step 4: Set up the equation for the initial elongation
Given that the initial elongation is 0.04 m, we can write:
0.04=4F⋅LY⋅πD2
Let's denote this as Equation (1).
Step 5: Analyze the new conditions
Now, the length and diameter of the wire are both doubled. Therefore, the new length L′=2L and the new diameter D′=2D.
Step 6: Calculate the new area
The new cross-sectional area A′ will be:
A′=π(D′)24=π(2D)24=π⋅4D24=πD2
Step 7: Set up the equation for the new elongation
Using the same formula for elongation with the new dimensions:
ΔL′=F⋅L′Y⋅A′=F⋅(2L)Y⋅(πD2)
Step 8: Substitute the new area into the elongation formula
Substituting the new area into the elongation formula, we have:
ΔL′=2F⋅LY⋅πD2
Step 9: Relate the new elongation to the initial elongation
From Equation (1), we know:
F⋅LY⋅πD2=0.01
Thus, we can express the new elongation as:
ΔL′=2⋅0.01=0.02 m
Conclusion
The new elongation in the wire when the length and diameter are doubled while applying the same force F is:
ΔL′=0.02 m
We have a wire with an elongation (ΔL) of 0.04 m when a force (F) is applied to it. We denote the original length of the wire as L and its diameter as D.
According to Hooke's Law, the elongation (ΔL) of a wire can be expressed as:
ΔL=F⋅LY⋅A
where:
- F is the applied force,
- L is the original length of the wire,
- Y is the Young's modulus of the material,
- A is the cross-sectional area of the wire.
A=πD24
Substituting the area into the elongation formula, we have:
ΔL=F⋅LY⋅(πD24)=4F⋅LY⋅πD2
Given that the initial elongation is 0.04 m, we can write:
0.04=4F⋅LY⋅πD2
Let's denote this as Equation (1).
Now, the length and diameter of the wire are both doubled. Therefore, the new length L′=2L and the new diameter D′=2D.
The new cross-sectional area A′ will be:
A′=π(D′)24=π(2D)24=π⋅4D24=πD2
Using the same formula for elongation with the new dimensions:
ΔL′=F⋅L′Y⋅A′=F⋅(2L)Y⋅(πD2)
Substituting the new area into the elongation formula, we have:
ΔL′=2F⋅LY⋅πD2
From Equation (1), we know:
F⋅LY⋅πD2=0.01
Thus, we can express the new elongation as:
ΔL′=2⋅0.01=0.02 m
The new elongation in the wire when the length and diameter are doubled while applying the same force F is:
ΔL′=0.02 m
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
At t=0, a constant force is applied on 3kg block. Find out maximum elongation in spring in cm.
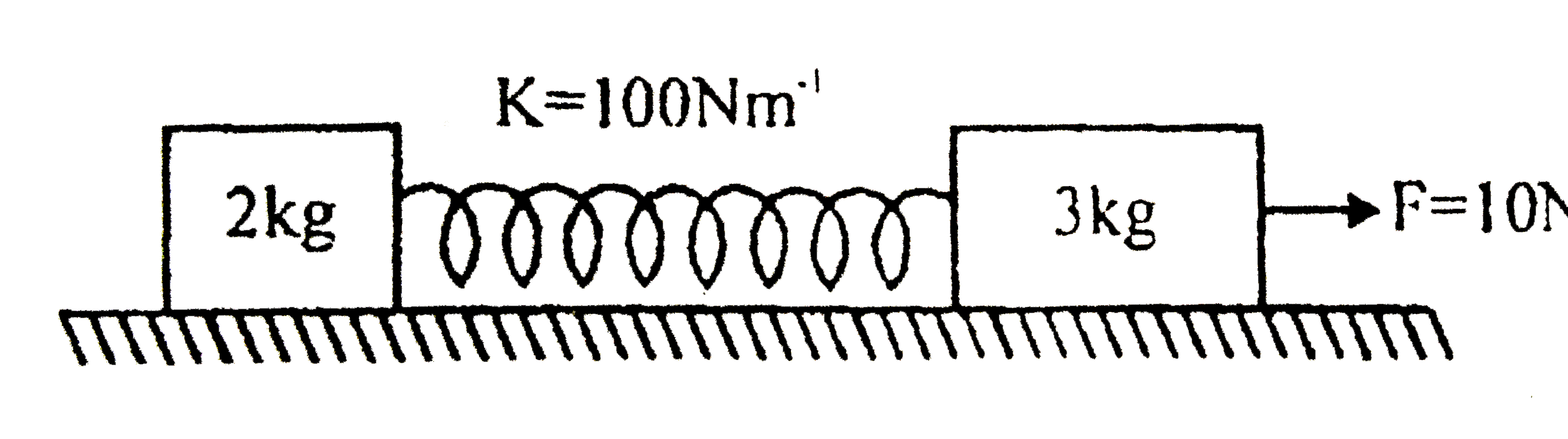
View SolutionA uniform metallic wire is elongated by 0.04 m when subjected to a linear force F. The elongation, if its length and diameter is doubled and subjected to the same force will be _____ cm.
View Solution
Knowledge Check
When a force is applied along the length of the wire
Athe length of the wire increases but its radius remains the sameBboth the ends of its length increases and radius also increasesClength increases but radius decreasesDboth length and radius decreasesWhen radius of wire is doubled, the elongation dl of the wire
Ais doubledBremains same.Cbecomes half.Dbecomes one fourthTwo blocks are in contact on a frictionless table. One has mass m and the other 2m. A force F is applied on 2m as shown in the figure. Now the same force F is applied from the right on m. In the two cases the ratio of force of contact between the two blocks will be
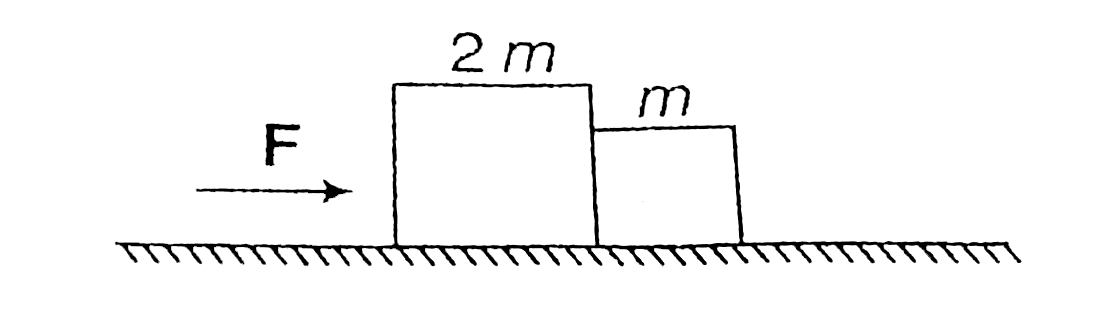 AsameB1:2C2:1D1:3
AsameB1:2C2:1D1:3
Two blocks are in contact on a frictionless table. One has mass m and the other 2m. A force F is applied on 2m as shown in the figure. Now the same force F is applied from the right on m. In the two cases the ratio of force of contact between the two blocks will be

View SolutionA brass wire of length 300cm when subjected to a force F produces an elongation a. Another wire of twice the diameter and of same length and material, when subjeceted to the force F produces and elongation b. Then the value of a/b is
View SolutionA force F is applied on the wire of radius r and length L and change in the length of wire is l. If the same force F is applied on the wire of the same material and radius 2r and length 2L. Then the change in length of the other wire is
View SolutionA wire of length L extends by l on application of force F. Suppose the wire is cut into 3 equal parts and the same force is applied to one of them. Now the extension will be
View SolutionA wire extends by 1mm when a force a applied. Double the force is applied to another wire of some material and length but half the radius of cross-section. The elongation of the wire in mm will be
View Solution
