A square of side a=12cm placed in Xy plane centre at origin . A charge q=12 μC place at z=6cm. If flux through square plate ix X×102, then find x: (##JM_21_M2_20210224_PHY_27_Q01.png" width="80%">
To solve the problem, we need to calculate the electric flux through a square plate placed in the xy-plane, with a charge located above it in the z-direction. We will use Gauss's Law to find the flux.
1. Identify the Given Values:
- Side of the square plate, a=12cm=0.12m
- Charge, q=12μC=12×10−6C
- Position of the charge, z=6cm=0.06m
2. Understand the Geometry:
- The square plate is centered at the origin in the xy-plane.
- The charge is located directly above the center of the square plate at a height of 6 cm.
3. Use Gauss's Law:
- Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Qenc divided by the permittivity of free space ε0:
Φ=Qencε0
- Here, we consider a cube of side length equal to the height of the charge above the square plate (6 cm) and the square plate itself.
4. Calculate the Total Flux:
- The total flux through the entire closed surface (the cube) is given by:
Φtotal=qε0
- The value of ε0 (permittivity of free space) is approximately 8.85×10−12C2/N m2.
5. Calculate the Flux through One Face of the Cube:
- Since the charge is at the center of the cube, the flux is uniformly distributed through all 6 faces of the cube. Therefore, the flux through one face (the square plate) is:
Φsquare=Φtotal6=q6ε0
6. Substituting the Values:
- Substitute q=12×10−6C and ε0=8.85×10−12C2/N m2:
Φsquare=12×10−66×8.85×10−12
7. Calculate the Value:
- Calculate Φsquare:
Φsquare=12×10−653.1×10−12≈2.259×105N m2/C
8. Express the Flux in the Required Form:
- The problem states that the flux is x×102. Thus, we can express:
Φsquare=2259×102
- Therefore, x=2259.
Final Answer:
The value of x is 2259.
- Side of the square plate, a=12cm=0.12m
- Charge, q=12μC=12×10−6C
- Position of the charge, z=6cm=0.06m
- The square plate is centered at the origin in the xy-plane.
- The charge is located directly above the center of the square plate at a height of 6 cm.
- Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Qenc divided by the permittivity of free space ε0:
Φ=Qencε0
- Here, we consider a cube of side length equal to the height of the charge above the square plate (6 cm) and the square plate itself.
- The total flux through the entire closed surface (the cube) is given by:
Φtotal=qε0
- The value of ε0 (permittivity of free space) is approximately 8.85×10−12C2/N m2.
- Since the charge is at the center of the cube, the flux is uniformly distributed through all 6 faces of the cube. Therefore, the flux through one face (the square plate) is:
Φsquare=Φtotal6=q6ε0
- Substitute q=12×10−6C and ε0=8.85×10−12C2/N m2:
Φsquare=12×10−66×8.85×10−12
- Calculate Φsquare:
Φsquare=12×10−653.1×10−12≈2.259×105N m2/C
- The problem states that the flux is x×102. Thus, we can express:
Φsquare=2259×102
- Therefore, x=2259.
The value of x is 2259.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Four point charges qA=2μC,qB=5μC,qC=2μCandqD=5μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the centre of the square ?
(##U_LIK_SP_PHY_XII_C01_E01_006_Q01.png" width="80%">
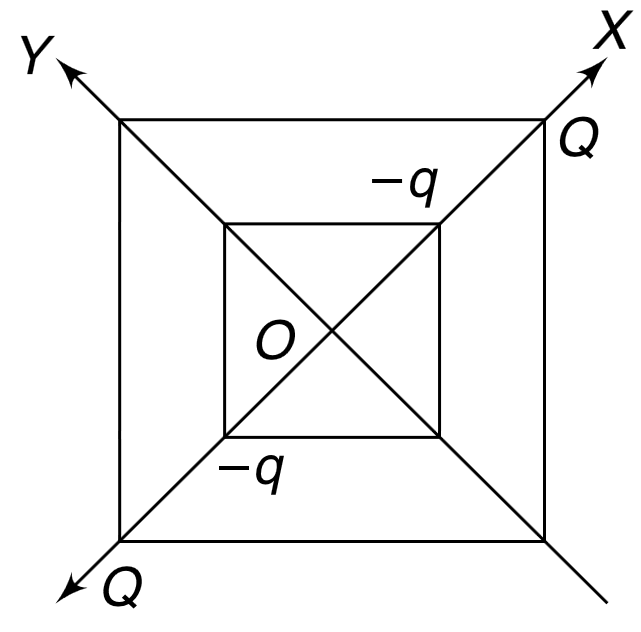
View SolutionTwo square of sides a and 2a are placed in xy plane with their centers at the origin. Two charges, – q each, are fixed at the vertices of smaller square (lying on X axis). Two charges, Q each, are fixed at the vertices of bigger square on the X axis (see figure). (a) Find work required to slowly move the larger square to infinity from the position shown. (b) Find work done by the external agent in slowly rotating the inner square by 90∘ about the Y axis followed by a rotation of 90∘ about the Z axis.
View Solution
Knowledge Check
Find the flux of point charge q through the square surface ABCD as shown (##JM21_M220210224_PHY09_Q01##)
A(A)q6ε0 (B)qε0 (C)q4ε0 (D)q2ε0BFind the flux of point charge q through the square surface ABCD as shown (##JM21_M220210224_PHY09_Q01##)Cnot varying with rDvarying as r2The major product of the following reaction is
(##MOD_SPJ_CHE_XII_P2_C12_E07_108_Q01.png" width="80%">A B
B C
C D
D
Find the coordinates of new square when ABCD is reflected through origin
(##CEN_JEE_MAT_X_C12_E01_025_Q01.png" width="80%">AA'≡(−2,−2),B'≡(−4,−2),C'≡(−4,−4),D'≡(−2,−4)BA'≡(2,2),B'≡(4,−2),C'≡(−4,−4),D'≡(−2,−4)CA'≡(−2,−2),B'≡(−4,−2),C'≡(4,4),D'≡(2,4)DA'≡(2,−2),B'≡(4,−2),C'≡(4,−4),D'≡(2,−4)
Five point charges each of charges +q are placed of five vertices of a regular hexagon of side 'l'. Find the magnitude of the resultant force on a charge -q placed at the centre of the hexagon.
(##U_LIK_SP_PHY_XII_C01_E09_018_Q01.png" width="80%">
View SolutionTwo charges +Q each ,are placed at the point A and B separated by a distancer r. A charge -q placed at the mid point of line AB is in a state of ____________ equilibrium.
(##U_LIK_SP_PHY_XII_C01_E05_006_Q01.png" width="80%">
View SolutionA point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
View SolutionIn figure , if AB = 12 cm , BC = 8 cm and AC = 10 cm , then AD is
(##CEN_JEE_MAT_X_C14_E01_035_Q01.png" width="80%">
View SolutionABC is an equilateral triangle. Charged of +q are placed at each corner. The electric field at O will be
(##U_LIK_SP_PHY_XII_C01_E04_006_Q01.png" width="80%">
View Solution
