The graph of v versus x in a SHM is (v: velocity, x= displacement)
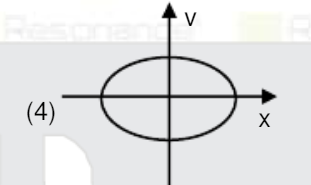
To solve the problem of finding the graph of velocity (v) versus displacement (x) in Simple Harmonic Motion (SHM), we can follow these steps:
1. Understand the relationship in SHM:
In SHM, the velocity (v) of a particle is related to its displacement (x) from the mean position. The formula for velocity in SHM is given by:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the displacement.
2. Square both sides:
To eliminate the square root, we square both sides of the equation:
v2=ω2(A2−x2)
3. Rearrange the equation:
Rearranging gives us:
v2ω2+x2A2=1
This is a standard form of the equation of an ellipse.
4. Identify the axes:
In this equation, if we let v represent the y-axis and x represent the x-axis, we can see that the equation describes an ellipse centered at the origin.
5. Conclusion:
Therefore, the graph of velocity versus displacement in SHM is an ellipse that passes through the origin.
Final Answer:
The correct option is that the graph of velocity versus displacement in SHM is an ellipse.
In SHM, the velocity (v) of a particle is related to its displacement (x) from the mean position. The formula for velocity in SHM is given by:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the displacement.
To eliminate the square root, we square both sides of the equation:
v2=ω2(A2−x2)
Rearranging gives us:
v2ω2+x2A2=1
This is a standard form of the equation of an ellipse.
In this equation, if we let v represent the y-axis and x represent the x-axis, we can see that the equation describes an ellipse centered at the origin.
Therefore, the graph of velocity versus displacement in SHM is an ellipse that passes through the origin.
The correct option is that the graph of velocity versus displacement in SHM is an ellipse.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
i.The acceleration versus time graph of a partical SHM is shown in the figure . Plot the displacement versus time graph
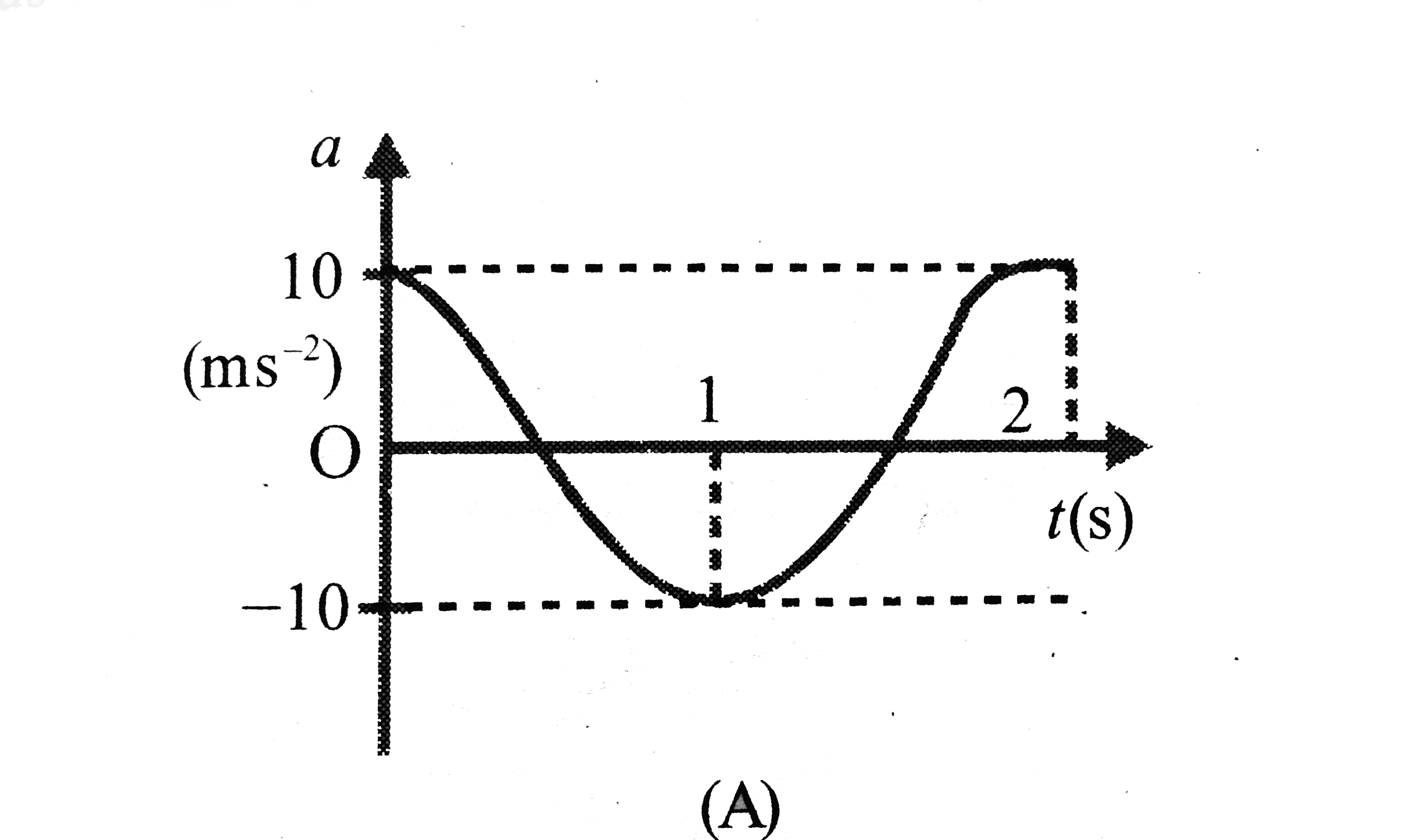
ii. The frection of oscillation is……..
iii. The displacement amplitude is ………
iv. At t=0, the velocity of the partical is ......
v. The kinetic energy of the partical is maximum at t=....... and t = ......
vi. The potential energy is maximum at t = ....... : t = ..... ans t = .........
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View Solution
Knowledge Check
A particle executes SHM. Then the graph of velocity as a function of displacement is
Aa straight lineBa circleCan ellipseDa hyperbolaA particle is executing SHM. Then the graph of velocity as a function of displacement is
Astraight lineBcircleCellipseDhyperbolaA particle executes SHM. Then the graph of velocity as a function of displacement is
AA circleBA parabolaCAn ellipseDA helix
Which of the following best represents the graph of velocity (v) versus displacement (s) for a particle travelling with an acceleration (uniform) and some non zero initial velocity?
View SolutionVariation of velocity v versus time t is ( Given x= Asinomegat)
View SolutionAcceleration v/s displacement graph of a particle moving in a straight line is as shown in the figure. The initial velocity of the particle is zero. The velocity v/s displacement graph of the particle would be :

View SolutionFor motion of an object along the x-axis the velocity v dipends on the displacement x an v=3x2, then what is the acceleration at x=2m.
View SolutionThe figure shows graph between velocity 'V' and displacement 'X' from mean position of a particle performing simple harmonic motion

The time period of motion of particle is:
View Solution
