When x is divided by 4 leaves remainder 3 then (2022+x)2022 is divisided by 8 , remainder is
The correct Answer is:A
To solve the problem, we need to find the remainder when (2022+x)2022 is divided by 8, given that x leaves a remainder of 3 when divided by 4.
1. Express x in terms of k:
Since x leaves a remainder of 3 when divided by 4, we can express x as:
x=4k+3
for some integer k.
2. Substitute x into the expression:
Now, substitute x into the expression 2022+x:
2022+x=2022+(4k+3)=2025+4k
3. Simplify modulo 8:
Next, we need to find 2025+4k modulo 8. First, we calculate 2025mod8:
2025÷8=253(integer part)
2025−(253×8)=2025−2024=1
Thus,
2025≡1mod8
Therefore,
2025+4k≡1+4kmod8
4. Consider 4kmod8:
The term 4k can take values 0 or 4 depending on whether k is even or odd:
- If k is even, 4k≡0mod8.
- If k is odd, 4k≡4mod8.
5. Combine results:
Therefore:
- If k is even:
1+4k≡1+0≡1mod8
- If k is odd:
1+4k≡1+4≡5mod8
6. Raise to the power of 2022:
Now we need to find (1+4k)2022mod8:
- If k is even:
(1)2022≡1mod8
- If k is odd:
(5)2022mod8
To find 52022mod8, we can observe the pattern:
51≡5mod8
52≡25≡1mod8
Since 52≡1mod8, all even powers of 5 will also be congruent to 1:
52022≡1mod8
7. Conclusion:
In both cases (whether k is even or odd), we find that:
(2022+x)2022≡1mod8
Therefore, the remainder when (2022+x)2022 is divided by 8 is:
1
Since x leaves a remainder of 3 when divided by 4, we can express x as:
x=4k+3
for some integer k.
Now, substitute x into the expression 2022+x:
2022+x=2022+(4k+3)=2025+4k
Next, we need to find 2025+4k modulo 8. First, we calculate 2025mod8:
2025÷8=253(integer part)
2025−(253×8)=2025−2024=1
Thus,
2025≡1mod8
Therefore,
2025+4k≡1+4kmod8
The term 4k can take values 0 or 4 depending on whether k is even or odd:
- If k is even, 4k≡0mod8.
- If k is odd, 4k≡4mod8.
Therefore:
- If k is even:
1+4k≡1+0≡1mod8
- If k is odd:
1+4k≡1+4≡5mod8
Now we need to find (1+4k)2022mod8:
- If k is even:
(1)2022≡1mod8
- If k is odd:
(5)2022mod8
To find 52022mod8, we can observe the pattern:
51≡5mod8
52≡25≡1mod8
Since 52≡1mod8, all even powers of 5 will also be congruent to 1:
52022≡1mod8
In both cases (whether k is even or odd), we find that:
(2022+x)2022≡1mod8
Therefore, the remainder when (2022+x)2022 is divided by 8 is:
1
Similar Questions
Knowledge Check
Is a two-digit integer 'x' dividible by 12?
I. When 'x' is divided by 5, the remainder is 2.
II. When 'x' is divided by 3, the remainder is 1.Aif the data in statement I alone are sufficient to answer the questin, while the data in statement II alone are not sufficient to answer the question.Bif the data in statement II alon are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question.Cif the data either in statement I alone or in statement II alone in sufficient to answer the question.Dif the data even in both the statements I and II together are not sufficient to answer the question.When
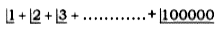 is divided by 8 then the remainder will be? A2B3C1D4
is divided by 8 then the remainder will be? A2B3C1D4A number which when divided by 32 leaves a remainder of 29. If this number is divided by 8 the remainder will be
A0B1C5D3
A number when divided by 195 leaves a remainder 47. If the same number is divided by 15, the remainder will be 1 (b) 2 (c) 3 (d) 4
View SolutionA number which when 'divided by 32 leaves a remainder of 29. If this number is divided by 8 the remainder will be
View SolutionWhat is the least possible number which when divided by 13 leaves the remainder 3 and when it is divided by 5 it leaves the remainder 2.
View SolutionA number which when divided by 10 leaves remainder of 9,when divided by 9 leaves remainder of 8 and when divided by 8 leaves a remainder of 7 is
View SolutionThe least number which when divided by 5, 6, 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder, is (a) 1677 (b) 1683 (c) 2523 (d) 3363
View Solution
