A block of mass, 2 kg is kept on a smooth surface as shown. It is being applied by a force F=20ˆi+10ˆj Find the displacement of the block in 10 seconds.
500m
10m
100m
50m
The correct Answer is:A
To solve the problem of finding the displacement of a block of mass 2 kg subjected to a force F=20^i+10^j over a time period of 10 seconds, we can follow these steps:
Step 1: Identify the Force Components
The force F has two components:
- In the x-direction: Fx=20N
- In the y-direction: Fy=10N
Step 2: Calculate the Acceleration
Using Newton's second law, we can find the acceleration a of the block. The formula is:
F=m⋅a
Where m is the mass of the block. Rearranging gives:
a=Fm
Calculating the acceleration in each direction:
- For the x-direction:
ax=Fxm=20N2kg=10m/s2
- For the y-direction:
ay=Fym=10N2kg=5m/s2
Step 3: Use the Kinematic Equation for Displacement
The displacement s can be calculated using the kinematic equation:
s=ut+12at2
Since the block starts from rest, the initial velocity u=0. Therefore, the equation simplifies to:
s=12at2
Step 4: Calculate Displacement in Each Direction
Now, we will calculate the displacement in both the x and y directions over the time period of t=10s.
- Displacement in the x-direction:
sx=12axt2=12⋅10m/s2⋅(10s)2=12⋅10⋅100=500m
- Displacement in the y-direction:
sy=12ayt2=12⋅5m/s2⋅(10s)2=12⋅5⋅100=250m
Step 5: Combine the Displacements
The total displacement vector →s is given by:
→s=sx^i+sy^j=500^i+250^jm
Final Answer
The displacement of the block in 10 seconds is:
→s=500^i+250^jm
---
The force F has two components:
- In the x-direction: Fx=20N
- In the y-direction: Fy=10N
Using Newton's second law, we can find the acceleration a of the block. The formula is:
F=m⋅a
Where m is the mass of the block. Rearranging gives:
a=Fm
Calculating the acceleration in each direction:
- For the x-direction:
ax=Fxm=20N2kg=10m/s2
- For the y-direction:
ay=Fym=10N2kg=5m/s2
The displacement s can be calculated using the kinematic equation:
s=ut+12at2
Since the block starts from rest, the initial velocity u=0. Therefore, the equation simplifies to:
s=12at2
Now, we will calculate the displacement in both the x and y directions over the time period of t=10s.
sx=12axt2=12⋅10m/s2⋅(10s)2=12⋅10⋅100=500m
sy=12ayt2=12⋅5m/s2⋅(10s)2=12⋅5⋅100=250m
The total displacement vector →s is given by:
→s=sx^i+sy^j=500^i+250^jm
The displacement of the block in 10 seconds is:
→s=500^i+250^jm
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
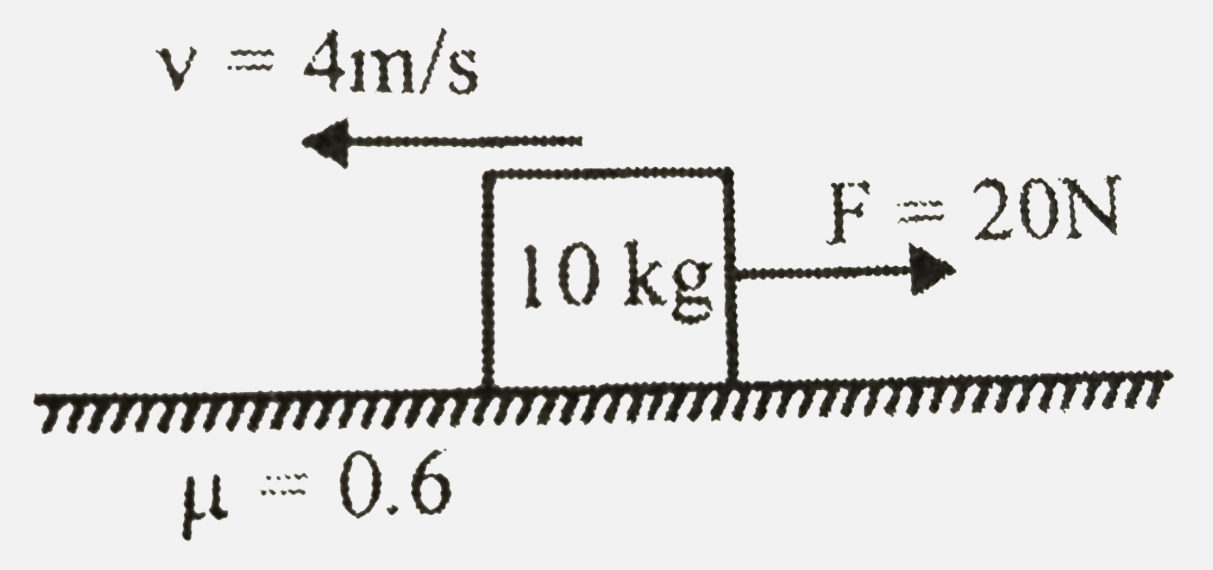
A block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View Solution
Knowledge Check
A block of mass 2 kg is resting on a smooth surface. At what angle a force of 10 N be acting on the block so that it will acquire a kinetic energy of 10 J after moving 2 m
A30∘B45∘C60∘D90∘A block of mass 20 kg is moving on a smooth surface by pulling through a light string of tension 10√2 N. Find the work done by string on the block for a displacement of 2 m along the surface.
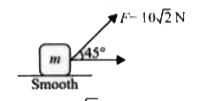 A10JB20√2JC20JD10√2J
A10JB20√2JC20JD10√2JA block of mass 10 kg is moving horizontally with a speed of 1.5 ms−1 on a smooth plane. If a constant vertical force 10N acts on it, the displacement of the block from the point of application of the force at the end of 4 second is
A5mB20 mC12 mD10 m
A block of mass 10 kg is kept over a rough surface and a force F=4t is applied on it. At what value of t the block will start moving :-

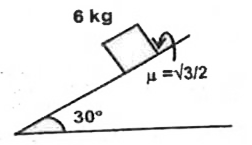
View SolutionA block of mass 6 kg is kept on rough surface as shown in figure. Find acceleration and friction force acting on the block. (Take g=10m/s2)
View SolutionA block of mass 10kg lying on a smooth horizontal surface is being pulled by means of a rope of mass 2kg .If a force of 36N is applied at the end of the rope,the tension at the midpoint of the rope is?
View SolutionA block of mass 10 kg is moving horizontally with a speed of 1.5 ms−1 on a smooth plane. If a constant vertical force 10N acts on it, the displacement of the block from the point of application of the force at the end of 4 second is
View SolutionA block of mass m kg is placed on a plank. The plank is moving with an acceleration 6ˆi+6ˆj (in m/s2 ). The frictional force acting on the block is (μ=0.5,g=10m/s2) :
View Solution
