The second derivative of the equation of a curve is given by the equation xd2ydx2=1, given by y=1, dydx=0 when x=1.
Find the equation of the curve.Solution in Malayalam
Step by step video & image solution for The second derivative of the equation of a curve is given by the equation x(d^2y)/(dx^2)=1, given by y=1, dy/dx=0 when x=1. Find the equation of the curve. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
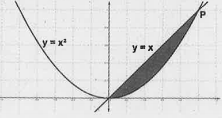
Consider the following figure
find the point of intersection (P) of the parabola and the line.
View SolutionFind the particular solution of the differential equation (x−y)dydx=x+2y, given that when x=1, y=0.
View SolutionSolve the differential equation xd2ydx2=1, given that y=1,dydx=0 when x=1
View SolutionSolve the differential equation: d2ydx2=x2+sin3x, given that dydx=1=y, when x=0
View SolutionWhich of the following are true for the curve represented by the differential equation sec2ydydx+2xtany=x3 satisfying y(1)=0 (A) equation of curve is 2tany=x2−1 (B) equation of curve is y2=x3−1 (C) curve is a parabola (D) curve is not a conic
View SolutionWhat is the equation of a curve passing through (0, 1) and whose differential equation is given by dy=ytanxdx?
View SolutionAn equation of the curve satisfying xdy−ydx=√x2−y2dx and y(1) = 0 is
View SolutionThe equation of curve passing through (0,1) which is a solution of differential equation (1+y2)dx+(1+x2)dy=0 is given by
View SolutionAn equation of the curve satisfying xdy−ydx=√x2−y2dx and y(1) = 0 is
View SolutionThe second derivative of the equation of a curve is given by the equation xd2ydx2=1, given by y=1, dydx=0 when x=1. Find the slope at x=e.
View SolutionThe second derivative of the equation of a curve is given by the equation xd2ydx2=1, given by y=1, dydx=0 when x=1.Find the equation of the normal at x=e.
View SolutionFind the particular solution ofthe differential equation (d^2y)/(dx^2) = 6x given that y = 1 and (dx)/(dy)= 2 when x = 0 .
View SolutionSolve the differential equation xd2ydx2=1, given that y=1,dydx=0 when x=1
View SolutionSolve the differential equation: d2ydx2=x2+sin3x, given that dydx=1=y, when x=0
View SolutionWhich of the following are true for the curve represented by the differential equation sec2ydydx+2xtany=x3 satisfying y(1)=0 (A) equation of curve is 2tany=x2−1 (B) equation of curve is y2=x3−1 (C) curve is a parabola (D) curve is not a conic
View Solution
