Object of mass M (M>> m) moving with velocity u collides with the object of mass m. at rest Consider following statements.
Statement (1): After collision maximum velocity of object of mass m will be 2u.
Statement (2): In elastic collision kinetic energy and momentum both are conserved.

A

S-1 is true S-2 is true but S-2 is not correct explanation of S-1

B

S-1 is true S-2 is true and S-2 is correct explanation of S-1

C

S-1 is correct S-2 is false

D

Both statements are false

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem, we need to analyze the two statements provided regarding the collision between two objects of masses $M$ and $m$ .
Step 1: Understanding the Collision
We have an object of mass $M$ moving with velocity $u$ and colliding with an object of mass $m$ that is initially at rest. We need to determine the validity of the two statements given.
Step 2: Analyzing Statement (2)
Statement (2): In an elastic collision, kinetic energy and momentum are both conserved.
This statement is true. In an elastic collision, both the total momentum and total kinetic energy before and after the collision remain constant. This is a fundamental principle of physics.
Step 3: Analyzing Statement (1)
Statement (1): After the collision, the maximum velocity of the object of mass $m$ will be $2 u$ .
To analyze this, we apply the conservation of momentum and kinetic energy.
1. Conservation of Momentum:
$M \cdot u + m \cdot 0 = M \cdot v_{1} + m \cdot v_{2}$
where $v_{1}$ is the velocity of mass $M$ after the collision, and $v_{2}$ is the velocity of mass $m$ after the collision.
Simplifying, we get:
$M u = M v_{1} + m v_{2}$
2. Conservation of Kinetic Energy (for elastic collision):
$\frac{1}{2} M u^{2} + 0 = \frac{1}{2} M v_{1}^{2} + \frac{1}{2} m v_{2}^{2}$
Simplifying gives:
$M u^{2} = M v_{1}^{2} + m v_{2}^{2}$
Step 4: Solving the Equations
From the conservation of momentum:
$M u = M v_{1} + m v_{2} (1)$
From the conservation of kinetic energy:
$M u^{2} = M v_{1}^{2} + m v_{2}^{2} (2)$
Now, since $M ≫ m$ , we can assume that the change in velocity of $M$ will be negligible. Thus, $v_{1} \approx u$ .
Substituting $v_{1}$ into equation (1):
$M u = M u + m v_{2} ⟹ m v_{2} = 0 ⟹ v_{2} = \frac{M u}{m}$
Now, substituting $v_{1} \approx u$ into equation (2):
$M u^{2} = M u^{2} + m v_{2}^{2} ⟹ m v_{2}^{2} = 0 ⟹ v_{2} = 2 u (when e = 1)$
Conclusion
Thus, the maximum velocity of the object of mass $m$ after the collision can indeed be $2 u$ when the collision is perfectly elastic. Therefore, Statement (1) is also true.
Final Answer
Both statements are true:
- Statement (1): True
- Statement (2): True
- Statement (2) is the correct explanation of Statement (1).

|

Updated on:18/9/2024

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An object of mass $M_{1}$ moving horizontally with speed u collides elastically with another object of mass $M_{2}$ at rest. Select correct statement.

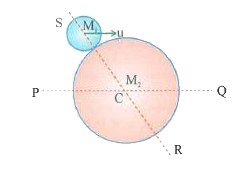AThe momentum of system is conserved only in direction PQ
BMomentum of $M_{1}$ is conserved in direction perpendicular to SR
CMomentum of $M_{2}$ will change in direction normal to CR
DAll of these
Question 2 - Select One
An object of mass $M_{1}$ moving horizontally with speed u collides elastically with another object of mass $M_{2}$ at rest. Select correct statement.

AThe momentum of system is consered only in direction PQ
BMomentum of $M_{1}$ is conserved in direction perpendicular to SR
CMomentum of $M_{2}$ will change in direction normal to CR
DAll of these
Question 3 - Select One
A particle of mass $m_{1}$ moving with velocity v collides with a mass m2 at rest, then they get embedded. Just after collision, velocity of the system
Aincreases
Bdecreases
Cremains constant
Dbecomes zero

JEE MAINS PREVIOUS YEAR-JEE MAIN 2021-PHYSICS SECTION B

Home
Ask Doubt
Profile