What is $R_{f}$ ?

Text Solution

Verified by Experts

$R_{f}$ means retardation factor. Its value in chromatography is ratio of distance moved by the substance and the solvent from base line.
$R_{f} = \frac{Distance moved by the substance from base line (x)}{Distance moved by the solvent from base line(y)}$

Updated on:21/07/2023

|

Class 11 CHEMISTRY ORGANIC CHEMISTRY – SOME BASIC PRINCIPLES AND TECHNIQUES

Topper's Solved these Questions

ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUESBOOK - KUMAR PRAKASHANCHAPTER - ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUESEXERCISE - Section-B - Match the following
28 Videos
ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUESBOOK - KUMAR PRAKASHANCHAPTER - ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUESEXERCISE - Section-B - State True or False For The Following Statements
42 Videos
ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUESBOOK - KUMAR PRAKASHANCHAPTER - ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUESEXERCISE - Section A -Try Your Self-3
20 Videos
HYDROGENBOOK - KUMAR PRAKASHANCHAPTER - HYDROGENEXERCISE - Section-D NCERT Exemplar (Long Answer)
8 Videos
QUESTION ASKED IN JEE -2018BOOK - KUMAR PRAKASHANCHAPTER - QUESTION ASKED IN JEE -2018EXERCISE - MCQ
10 Videos

Similar Questions

Knowledge Check

A substance is analyzed by paper chromatography, giving the chromatogram shown.

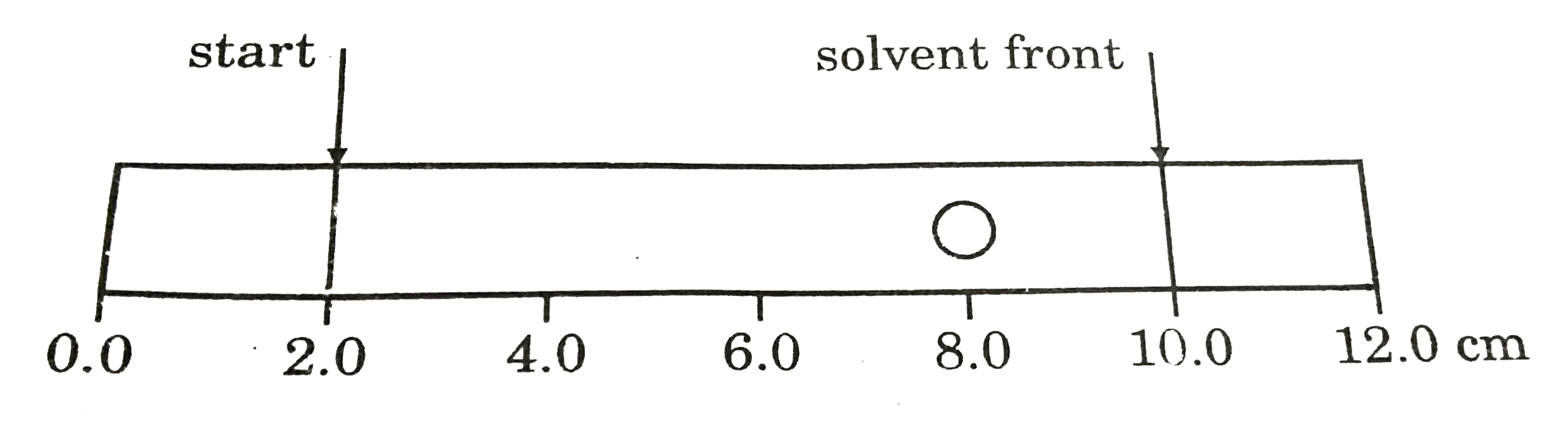
What is the $R_{f}$ value of the substance represented by the spot at 8.0 cm?
A $0.80$
B $0.75$
C $0.67$
D $0.60$
Let $f : R \to R$ be a function such that $f (x) = x^{3} + x^{2} f' (1) + x f'' (2) + f''' (3)$ for $x \in R$
What is f(1) equal to :
A $- 2$
B $- 1$
C0
D4
Let $f : R \to R$ be a function such that $f (x) = x^{3} + x^{2} f' (1) + x f'' (2) + f''' (3)$ for $x \in R$
What is $f' (1)$ is equal to ?
AA) $- 5$
BB) $- 1$
CC) $1$
DD) $0$

KUMAR PRAKASHAN-ORGANIC CHEMISTRY SOME BASIC PRINCIPLES AND TECHNIQUES-Section-B (Short Questions)

Home
Ask Doubt
Profile