यदि f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩e−|x|,−5<x<0−e−|x−1|+e−1+1,0≤x<2e−|x−2|,2≤x<4 अंतराल (−5,4) में f(x) की संतता और अवकलनीयता की जाँच कीजिये।
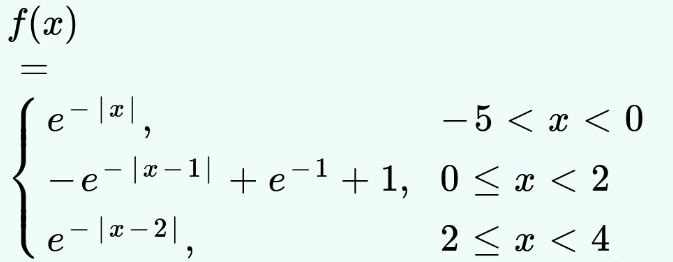
हम जानते हैं कि, |x−1|= {x−1x≥1−x+1x<1
अतः
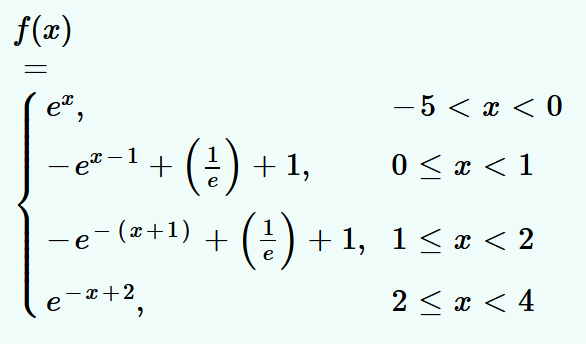
अतः 0,1,2 पर संतता की जांच करनी है।
x=0 पर,
LHL=limx→0ex
=e0
LHL=1
RHL
=limx→0−ex−1+(1e)+1
RHL=−e0−1+(1e)+1
RHL=−e−1+(1e)+1
RHL=−1e+1e+1=1
तथा f(0)=−e−1+(1e)+1
=1
स्पष्ट है कि,
LHL=RHL=f(x)=1
अतः x=0 पर संतत हैं|
इसी प्रकार x=1 पर,
LHL
=limx→1−ex−1+(1e)+1
LHL=−e1−1+(1e)+1
LHL=−e0+(1e)+1
LHL=−1+1e+1=1e
RHL
=limx→1−e−x+1+(1e)+1
RHL=−e−1+1+(1e)+1
RHL=−1+1e+1=1e
तथा f(1)=1e
स्पष्ट है कि,
LHL=RHL=f(x)=1e
अतः x=1 पर संतत हैं|
इसी प्रकार,
x=2 पर,
LHL
=limx→2−e−x+1+(1e)+1
LHL=−e−2+1+(1e)+1
LHL=−1e+(1e)+1
LHL=1
RHL
=limx→2−e−x+2
RHL=−e−2+2=1
RHL=−e0=1
RHL=1
तथा f(2)=1
स्पष्ट हैं की,
LHL=RHL=f(x)
अतः x=2 पर संतत हैं|
इसलिए f(x) संतत हैं, x=0,1,2
अवकलनीयता की जाँच,
चूंकि फलन हर जगह संतत हैं अतः फलन का हम सीधा अवकलन कर सकते हैं|
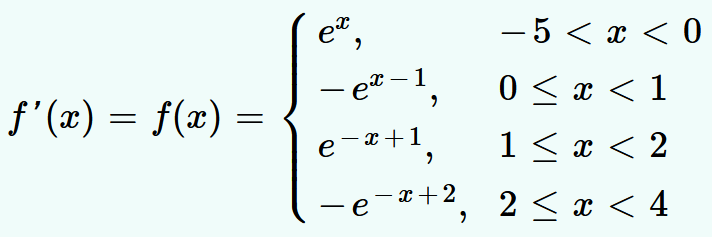
x=0 पर अवकलनीयता की जाँच,
LHD=limx→0ex
LHD=e0=1
RHD=limx→0−ex−1
RHD=−e0−1
RHD=−e−1=−1e
स्पष्ट हैं की,
LHD≠RHD अतः x=0 पर, अवकलनीय नहीं हैं|
इसी प्रकार x=1 पर
LHD=limx→1−ex−1
LHD=−e1−1
LHD=−e0=−1
RHD=limx→1e−x+1
RHD=e−1+1
RHD=e0=1
स्पष्ट है कि,
LHD≠RHD अतः x=1 पर, अवकलनीय नहीं हैं|
इसी प्रकार x=2 पर,
LHD=limx→2e−x+1
LHD=e−2+1= 1/e
RHD=limx→2−e−x+2
RHD=−e−2+1=−1e
स्पष्ट है कि,
LHD≠RHD अतः x=2 पर, अवकलनीय नहीं हैं|
अतः 0,1,2 पर संतत हैं परंतु अवकलनीय नहीं हैं|
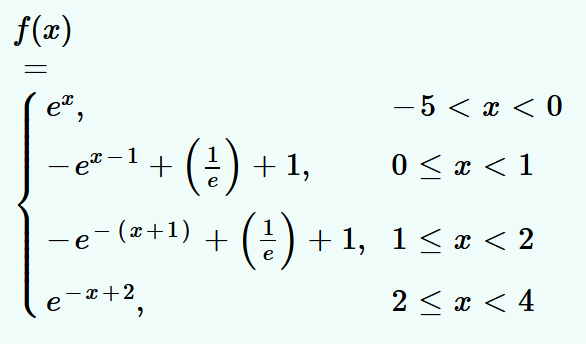
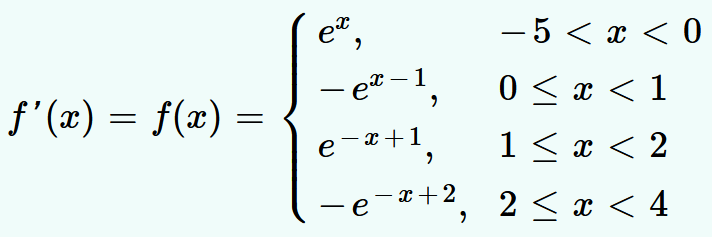
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - DIFFERENTIABILITYEXERCISE - Do Yourself-12videos
DIFFERENTIABILITY
- BOOK - ALLEN HINDICHAPTER - DIFFERENTIABILITYEXERCISE - Do Yourself-21videos
DIFFERENTIABILITY
- BOOK - ALLEN HINDICHAPTER - DETERMINANTEXERCISE - DO YOURSELF -91videos
DETERMINANT
- BOOK - ALLEN HINDICHAPTER - DIFFERENTIAL EQUATIONEXERCISE - EXERCISE-05[B] (JEE(ADVANCED) : PREVIOUS YEAR QUESTIONS)23videos
DIFFERENTIAL EQUATION
Similar Questions
माना फलन f(x)={x3,x2<1x,x2≥1,x=1 पर अवलनीयता की जाँच कीजिये ।
04:43View Solutionयदि फलन f(x)={(x−1)|x−1|,x≠10,x−1,x=1 पर संतत और अवकलनीयता की जाँच कीजिये।
02:37View Solutionसमीकरण निकाय λx+y+z=0,−x+λy+z=0,−x−y+λz=0 का एक अशून्य हल होगा यदि λ का वास्तविक मान है
01:28View Solutionएक देश में 10% खाद्यान्न की कमी है। इसकी जनसंख्या में 3% प्रतिवर्ष वृद्धि होती है तथा अन्न उत्पादन में गत वर्ष की तुलना में प्रतिवर्ष वृद्धि 4% है। यदि प्रति व्यक्ति औसतन खाद्यान्न आवश्यकता समान है तो सि कीजिए कि n वर्षों पश्चात् देश, खाद्यान्न में पूर्णतया आत्म निर्भर हो जाएगा जहाँ n वह न्यूनतम पूर्णांक है जो कि ln10−ln9ln(1.04)−0.03 से अधिक या बराबर है।
02:31View SolutionFind the value of a + b if f(x) = {((a e^(1//|x+2|) - 1)/(2-e^(1//|x+2|)),; -3 lt x lt -2), (b,; x = -2), (sin((x^4-16)/(x^5+32)),; -2 lt x lt 0):} is continuous at x = -2.
03:51View SolutionIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩ex,0≤x<12−ex−1,1<x≤2andg(x)=∫x0f(t)dt,x−e,2<x≤3
x∈[1,3], then02:05View SolutionIf f(x)=⎧⎪⎨⎪⎩x−5forx≤14x2−9for1<x<2 then f'(2+)3x+4forx≥2 =
01:28View SolutionIf f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩4−3<x<−15+x−1≤x<05−x0≤x<2x2+x−32<x<3 then, f(|x|) is
01:55View Solutionफलन f(x) की x=1 तथा x=2 पर सततता का परीक्षण कीजिये , यदि f(x)=⎧⎪⎨⎪⎩0,if 0<x<1x,if 1≤x<2x3/4,if 2≤x<3
06:44View SolutionIf f(x)=⎧⎪⎨⎪⎩x, for 0≤x<12, for x=1x+1, for 1<x≤2, then f is
01:19View SolutionIf f(x)={x,when 0<x<12−x,when1<x≤2then f'(1) is equal to-
05:29View SolutionIf f(x) {1for −π2<x<01+sinxfor0≤x<π2,then at x= 0 ,f'(x) -
04:30View SolutionThe cumculative distribution function of a discrete random variable is given by
F(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0for −∞<x<012for 0≤x<135for 1≤x<245for 2≤x<3910for 3≤x<41for 4≤x<∞
Find (i) the probability mass function (ii) P(X<3) and (iii) P(X≥2).08:20View SolutionIf f(x)=∫ex(x−1)(x−2)dx, then show that f(x) is a decreasing function 1<x<2.
02:08View Solutionफलन के लिए रोल प्रमेय की सत्यता की जाँच कीजिए
f(x)=⎧⎪⎨⎪⎩x2+10≤x≤1यदि3−x1<x≤204:59View Solution

