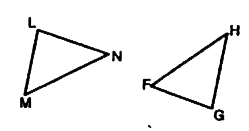
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚ ਤੁਸੀਂ ਕਿਹੜੇ ਸਰਬੰਗਸਮ ਮਾਪ ਦੰਡ ਦਾ ਪ੍ਰਯੋਗ ਕਰੋਗੇ? ਦਿੱਤਾ ਹੈ: ∠MLN=∠FGH ∠NML=∠GFH ML=FG ਇਸ ਲਈ ,△LMN≅△GFH
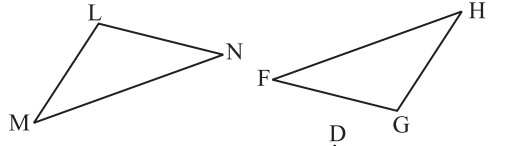
Step by step video & image solution for ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚ ਤੁਸੀਂ ਕਿਹੜੇ ਸਰਬੰਗਸਮ ਮਾਪ ਦੰਡ ਦਾ ਪ੍ਰਯੋਗ ਕਰੋਗੇ? ਦਿੱਤਾ ਹੈ: angle MLN = angle FGH angle NML = angle GFH ML = FG ਇਸ ਲਈ ,triangle LMN cong triangle GFH by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
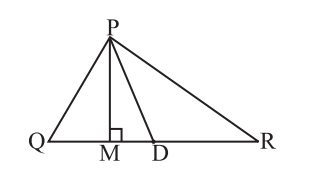
△PQR ਵਿੱਚ ਭੁਜਾ ¯¯¯¯¯¯QR ਦਾ ਮੱਧ ਬਿੰਦੂ D ਹੈ। ¯¯¯¯¯¯¯PM___________ ਹੈ।
View Solutionਇੱਕ ਆਇਤਾਕਾਰ (ਖੇਤ) ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਕ੍ਰਮਵਾਰ : 500 ਮੀ. ਅਤੇ 300 ਮੀ. ਹੈ। ਪਤਾ ਕਰੋ:- (i) ਖੇਤ ਦਾ ਖੇਤਰਫਲ (ii) ਖੇਤ ਜਾਂ ਜਮੀਨ ਦਾ ਮੁੱਲ, ਜੇਕਰ 1 ਮੀ2 . ਜਮੀਨ ਦਾ ਮੁੱਲ ₹10,000 ਰੁ. ਹੋਵੇ।
View SolutionGlancing angle and angle of incidence are ______ angle.
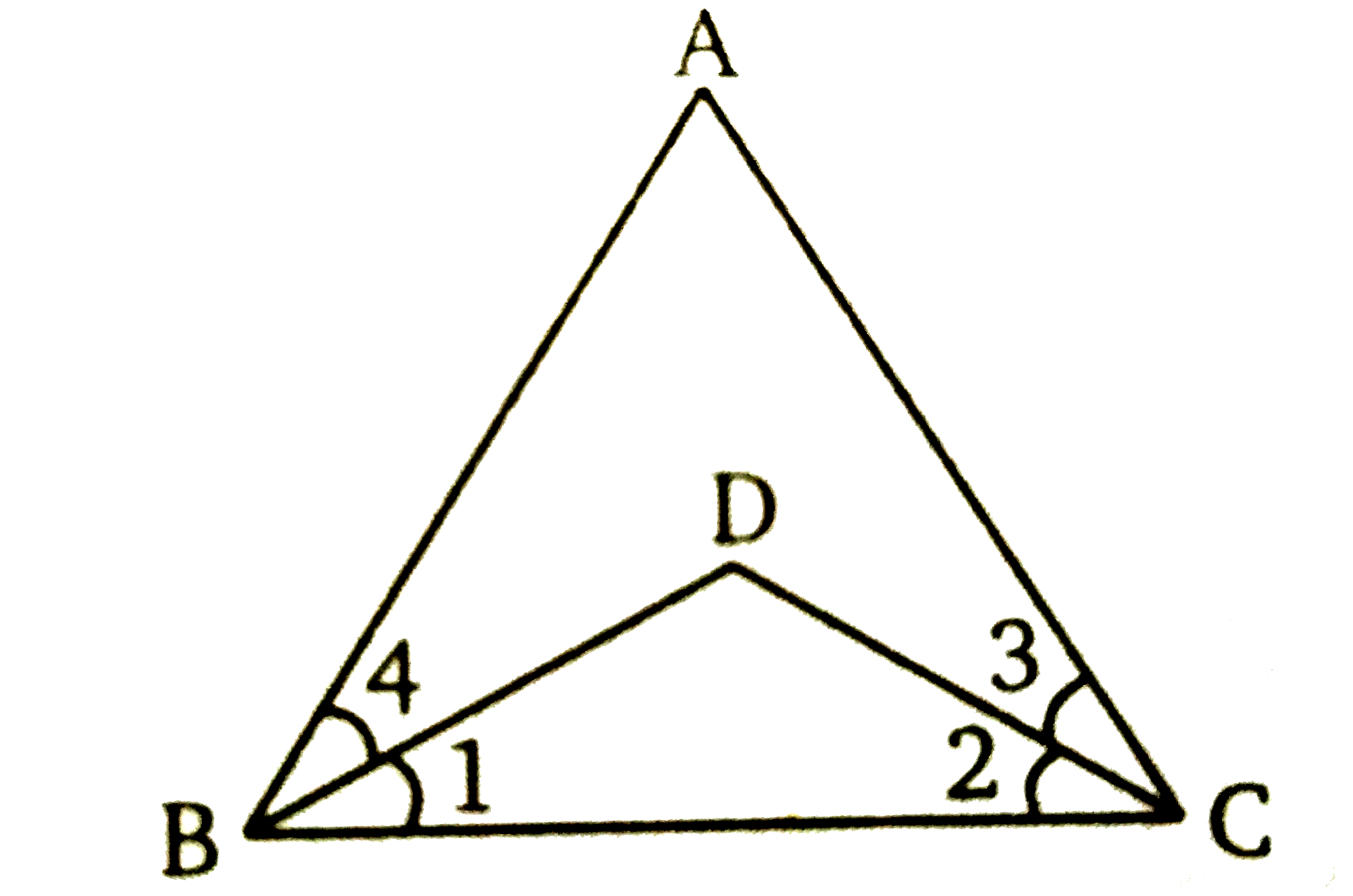
View Solutionसंलग्न चित्र में यदि ∠ABC=∠ACB,∠3=∠4, तब सिद्ध कीजिए कि ∠1=∠2
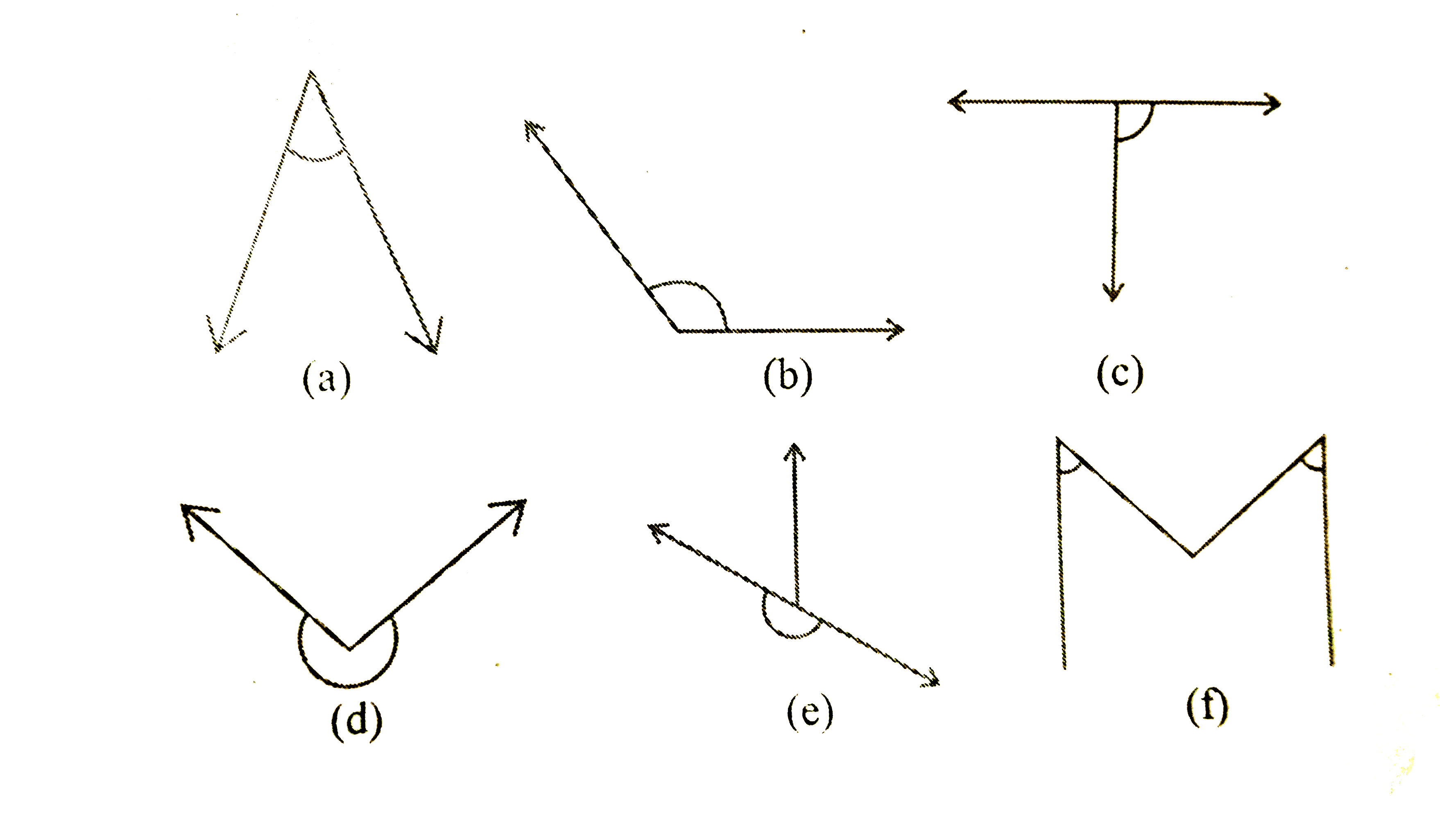
View Solutionनिम्न में से प्रत्येक कोण को समकोण, ऋजुकोण, न्यूनकोण, अधिक कोण या प्रतिवर्ती कोण के रूप में वर्गीकृत कीजिए :
View SolutionTwo triangles LMN and FHG are given, ML=FG , ∠MLN=∠FGH and ∠NML=∠GFH. So, △LMN≅△GFH by which rule?
View Solutionनिम्न में आप कौन से सर्वांगसम प्रतिबंधों का प्रयोग करेंगे ?
दिया है : ∠MLN=∠FGH,∠NML=∠GFH,ML=FG
इसलिए, ΔLMN≅ΔGFH
View Solutionकिसी कोण के लंबपूरक कोण तथा ऋजुपुरक कोण का अनुपात 2 : 5 है , तो वह कोण ज्ञात कीजिए।
View SolutionIn a ΔABC∠A+∠B=145∘,2∠B+∠C=180∘ Find ∠Aand∠B
View Solutionनिम्न में आप कौन सा सर्वांगसम प्रतिबंधो का प्रयोग करेंगे ?
दिया हैं : ∠MLN=∠FGH, ∠NML=∠GFH,ML=FG इसलिए , ΔLMN≅ΔGFH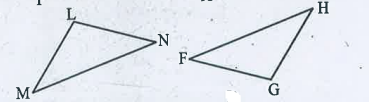
View Solutionকোণের মান অনুযায়ী ছোটো থেকে বড়ো সাজাও : সরলকোণ, সূক্ষ্মকোণ, প্রবৃদ্ধ কোণ, স্থূলকোণ, সমকোণ ।
View Solutionকোনো কোণের পূরক কোণ সেই কোণটিই হলে কোণটির বৃত্তীয় মান—
View Solutioncontour line DE | | रेख GF Is. Kiran EG and Kiran FG are respectively angle DEF And angle DFM These angles are divisors. So prove that (i) angle DEF = angle EDF , (ii) EF=FG
View SolutionGlancing angle and angle of incidence are _______ angles .
View Solution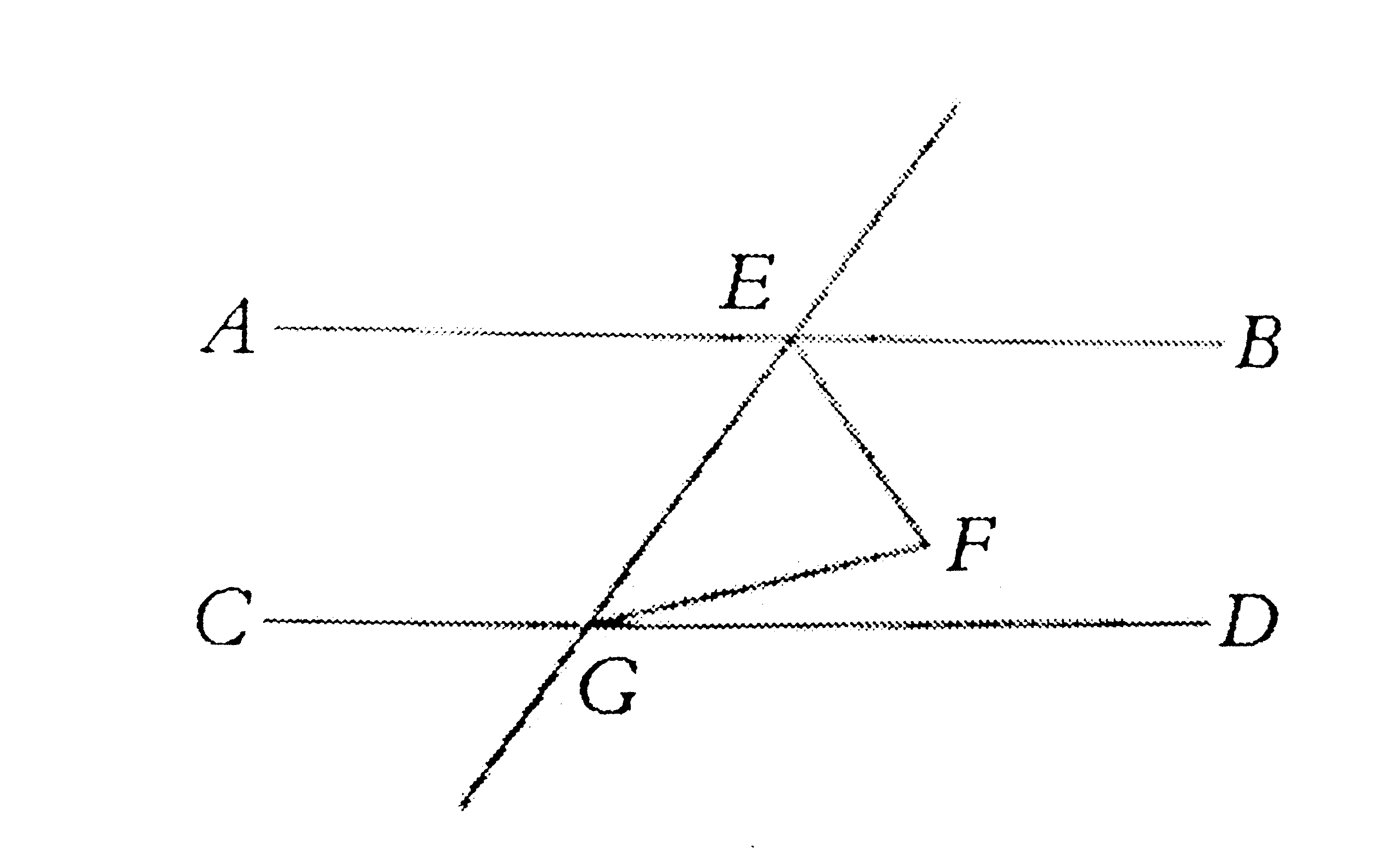
In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.
View Solution
