ਨਿਮਨ ਲਿਖਤ ਫਲਨ ਦੀ ਲਗਾਤਾਰਤਾ ਤੇ ਵਿਚਾਰ ਕਰੋ: f(x)=sinx⋅cosx
Step by step video & image solution for ਨਿਮਨ ਲਿਖਤ ਫਲਨ ਦੀ ਲਗਾਤਾਰਤਾ ਤੇ ਵਿਚਾਰ ਕਰੋ: f(x) = sinx cdot cosx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ਲਗਾਤਾਰਤਾ ਅਤੇ ਡਿਫ਼ਰੈਂਸ਼ੀਏਬਿਲਿਟੀBOOK - PSEB (PUNJABI MEDIUM)CHAPTER - ਲਗਾਤਾਰਤਾ ਅਤੇ ਡਿਫ਼ਰੈਂਸ਼ੀਏਬਿਲਿਟੀEXERCISE - Exercise
112 Videos
- ਰੈਖਿਕ ਪ੍ਰੋਗਰਾਮਿੰਗBOOK - PSEB (PUNJABI MEDIUM)CHAPTER - ਰੈਖਿਕ ਪ੍ਰੋਗਰਾਮਿੰਗEXERCISE - Exercise
17 Videos
- ਵੈਕਟਰਾਂ ਦਾ ਬੀਜ ਗਣਿਤBOOK - PSEB (PUNJABI MEDIUM)CHAPTER - ਵੈਕਟਰਾਂ ਦਾ ਬੀਜ ਗਣਿਤEXERCISE - Exercise
58 Videos
Similar Questions
x=3 ਤੇ ਫਲਨ f(x)=2x2−1 ਦੀ ਲਗਾਤਾਰਤਾ ਦੀ ਜਾਂਚ ਕਰੋ।
View Solutionਨਿਮਨਲਿਖਤ ਪ੍ਰਤਿਬੰਧਾਂ ਦੇ ਬਾਬਤ Z=3x+4y ਦਾ ਅਧਿਕਤਮੀਕਰਣ ਕਰੋ: x+y≤4,x≥0,y≥0
View Solutionਉੱਤਰ ਤੋਂ 30o ਪੂਰਬ ਵਿੱਚ 40 km ਦੇ ਵਿਸਥਾਪਨ ਦਾ ਗ੍ਰਾਫ ਨਿਰੂਪਨ ਕਰੋ।
View SolutionFind the period of the following function
(i) f(x)=|sinx|+|cosx|
(ii) f(x)=cos(cosx)+cos(sinx)
(iii) f(x)=|sinx+cosx||sinx|+|cosx|
View Solutionयदि F(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ है, तो सिद्ध कीजिए कि
View SolutionIf f(x) =∣∣ ∣∣sinxcosxsinxcosx−sinxcosxx11∣∣ ∣∣ find the value of 2(f'(o))+{f'(1)}2
View SolutionIf A=[1242], then show that |2A|=4|A|.
View SolutionIf f(x)=∣∣ ∣∣cosxcosxsinx−cosxcosx−sinxsinxsinxcosx∣∣ ∣∣, then find its determinant
View Solutionयदि f(x)=sinx−cosxsinx+cosx, तो मान निकालें f(π3).
View Solutionf(x)=(|sinx|+|cosx|)/(|sinx-cosx|) Is a period of
View SolutionFind the period of the following function
(i) f(x)=|sinx|+|cosx|
(ii) f(x)=cos(cosx)+cos(sinx)
(iii) f(x)=|sinx+cosx||sinx|+|cosx|
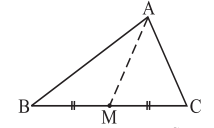
View Solutionਤ੍ਰਿਭੁਜ ABC ਦੀ ਇੱਕ ਮੱਧਿਕਾ AM ਹੈ। ਦੱਸੋ ਕਿ AB+BC+CA>2AM?(ਸੰਕੇਤ:triangleABMਅਤੇtriangle AMC ਦੀਆਂ ਭੁਜਾਵਾਂ ਉੱਪਰ ਵਿਚਾਰ ਕਰੋ।)
View SolutionSuppose A = {– 1, 0, 1, 2} , B = {– 4, – 2, 0, 2} And f, g : A rarr B , Respectively f (x) = x^2 – x , x in A And g (x) = 2 | x- (1/2) | -1, x in A ਰਾਹੀਂ ਪਰਿਭਾਸ਼ਿਤ ਫਲਨ ਹਨ, ਕੀ f ਅਤੇ g ਆਪਣੇ ਉੱਤਰ ਦੀ ਪੁਸ਼ਟੀ ਕਰੋ।
View SolutionIf A=⎛⎜⎝cosxsinx0−sinxcosx0001⎞⎟⎠=f(x) then A−1=
View SolutionIf F(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ and G(x)=⎡⎢⎣cosx0sinx010−sinx0cosx⎤⎥⎦ then [F(x)G(x)]−1=
View Solution
