Superposition Principle

Class 12 PHYSICS CURRENT ELECTRICITY

Knowledge Check

Consider a block of conducting material of resistivity $' ρ'$ shown in the figure. Current $' I'$ enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage $Δ V$ developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law $E = ρ j,$ where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.

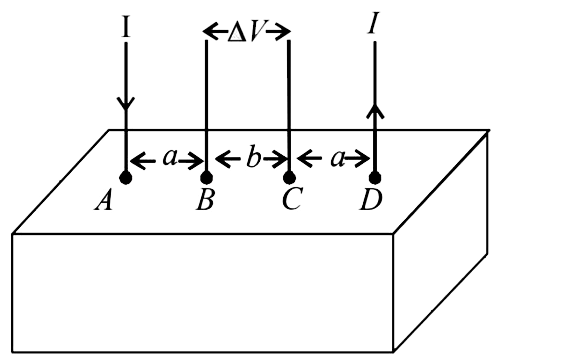
Delta V measured between B and C is
A $\frac{ρ I}{π a} - \frac{ρ I}{π (a + b)}$
B $\frac{ρ I}{a} - \frac{ρ I}{a + b}$
C $\frac{ρ I}{2 π a} - \frac{ρ I}{2 π (a + b)}$
D $\frac{ρ I}{2 π (a - b)}$
Consider a block of conducting material of resistivity $' ρ'$ shown in the figure. Current $' I'$ enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage $Δ V$ developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law $E = ρ j,$ where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.

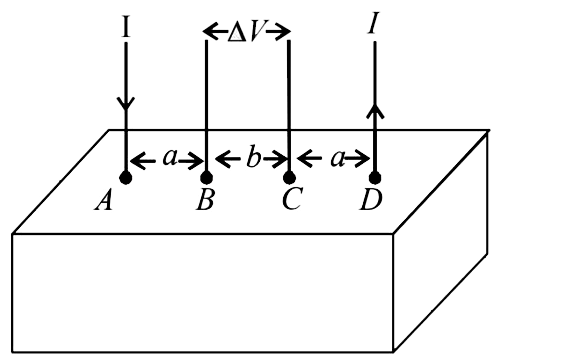
For current entering at A, the electric field at a distance 'r'
A $\frac{ρ I}{8 π r^{2}}$
B $\frac{ρ I}{r^{2}}$
C $\frac{ρ I}{2 π r^{2}}$
D $\frac{ρ I}{4 π r^{2}}$

Superposition Principle

Similar Questions

Knowledge Check

Recommended Questions