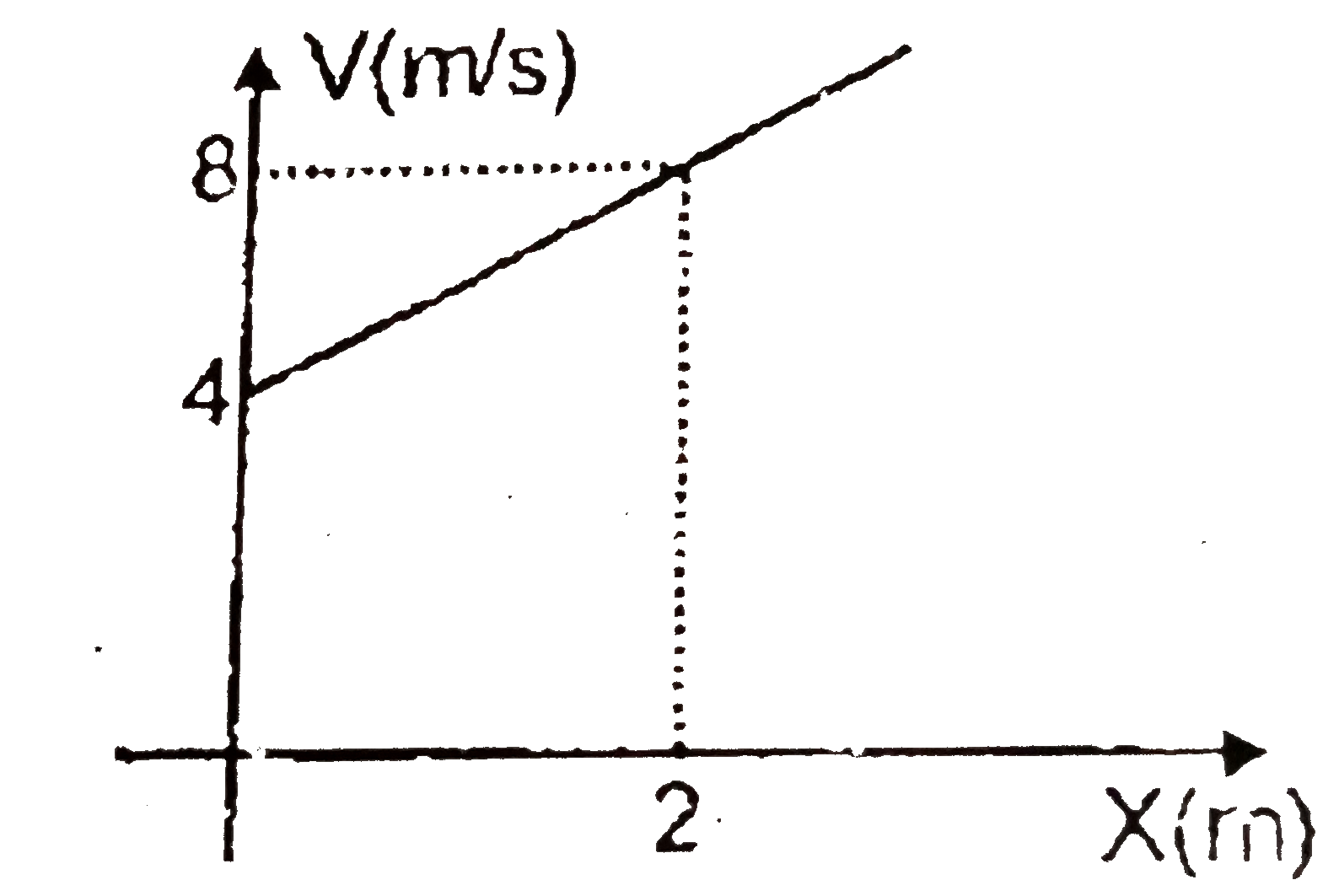
Velocity v/s position graph of a body performing SHM is
elipse
circle
parabola
straight line
The correct Answer is:A
To solve the problem of determining the velocity vs. position graph of a body performing Simple Harmonic Motion (SHM), we can follow these steps:
1. Understanding Simple Harmonic Motion (SHM):
- In SHM, a body oscillates about an equilibrium position. The maximum displacement from this equilibrium position is called the amplitude (A).
2. Velocity in SHM:
- The velocity (v) of a body in SHM can be expressed as:
v=ω√A2−x2
where:
- ω is the angular frequency,
- A is the amplitude,
- x is the displacement from the equilibrium position.
3. Rearranging the Velocity Equation:
- Squaring both sides gives:
v2=ω2(A2−x2)
- Rearranging this, we find:
v2+ω2x2=ω2A2
4. Identifying the Graph:
- This equation resembles the standard equation of an ellipse:
x2A2+v2ω2A2ω2=1
- Here, A is the semi-major axis and Aωω is the semi-minor axis.
5. Conclusion:
- The graph of velocity (v) versus position (x) for a body performing SHM is an ellipse centered at the origin.
Final Answer:
The velocity vs. position graph of a body performing Simple Harmonic Motion is an ellipse.
---
- In SHM, a body oscillates about an equilibrium position. The maximum displacement from this equilibrium position is called the amplitude (A).
- The velocity (v) of a body in SHM can be expressed as:
v=ω√A2−x2
where:
- ω is the angular frequency,
- A is the amplitude,
- x is the displacement from the equilibrium position.
- Squaring both sides gives:
v2=ω2(A2−x2)
- Rearranging this, we find:
v2+ω2x2=ω2A2
- This equation resembles the standard equation of an ellipse:
x2A2+v2ω2A2ω2=1
- Here, A is the semi-major axis and Aωω is the semi-minor axis.
- The graph of velocity (v) versus position (x) for a body performing SHM is an ellipse centered at the origin.
The velocity vs. position graph of a body performing Simple Harmonic Motion is an ellipse.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Knowledge Check
Velocity v/s Position graph of a particle performing curvilinear motion is as shown. Then select the CORRECT statement:
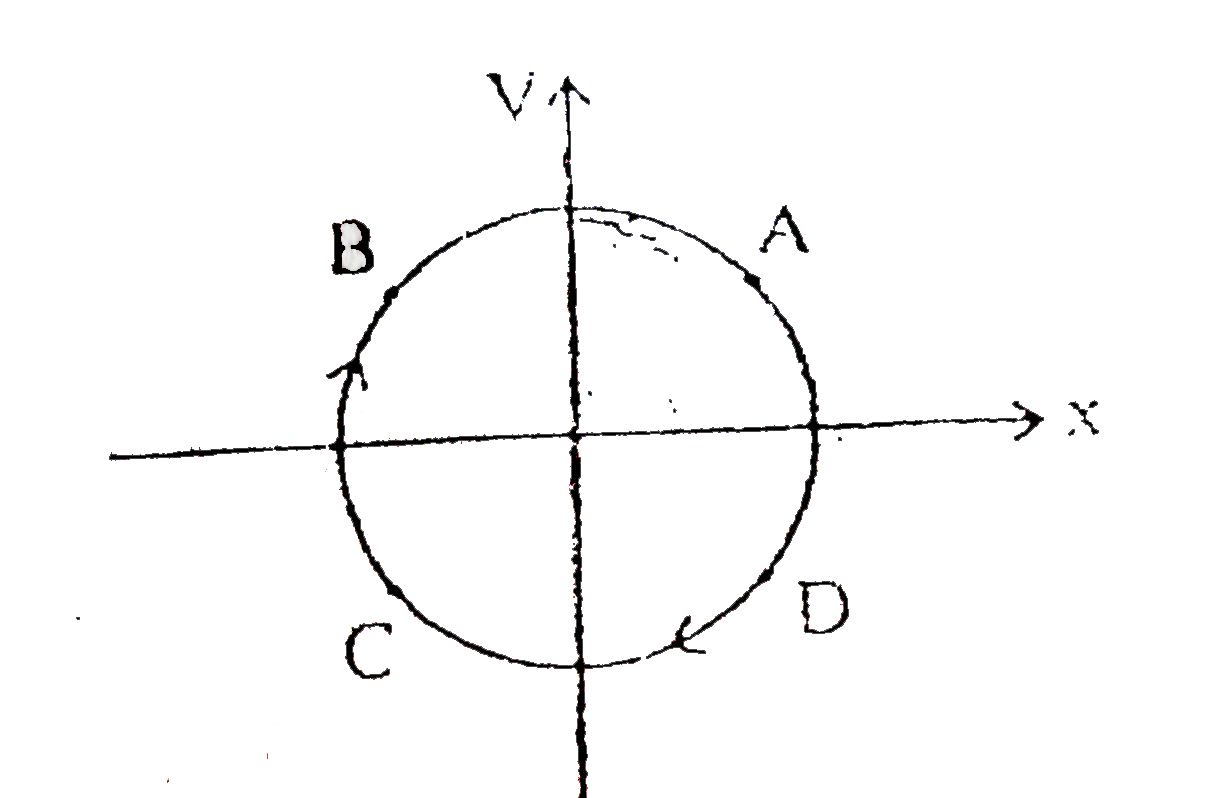 AParticle moves with constant speed through out the motionBAt B particle is moving towards the origin with increasing speed.CAt B particle is moving away from origin with decreasing speedDData insufficfient
AParticle moves with constant speed through out the motionBAt B particle is moving towards the origin with increasing speed.CAt B particle is moving away from origin with decreasing speedDData insufficfientA body is performing SHM, then its
Aaverage total enregy per cycle is equal to its maximum kinetic energyBaverage kinetic energy per cycle is equal to half of its maximum kinetic energyCmean velocity over a complete cycle is equal to 2π times of maximum velocityDroot mean square velocity is 1√2 times of its maximum velocityA body is performing SHM, then its
Aaverage total energy per cycle is equal to its maximum kinetic energyBaverage kinetic energy per cycle is equal to half of its maximum kinetic energyCmean velocity over a complete cycle is equal to 2π times of its maximum velocityDroot meqan square velocity is 1√2 times of its maximum velocity
Displacement time graph of particle performing SHM is as shown in figure. Assume that mean position is at x=0
View SolutionVelocity at mean position of a particle executing SHM is v. Velocity of the particle at a distance equal to half of the amplitude will be
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
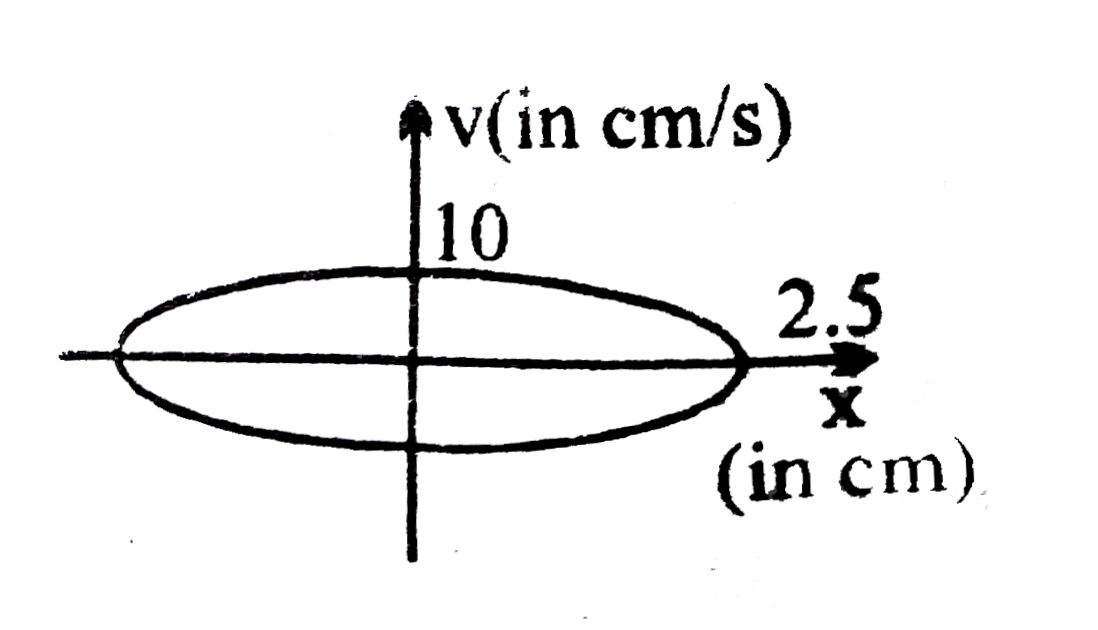
View SolutionThe amplitude of particle performing S.H.M. is
View SolutionThe graph between instantaneous velocity and acceleration of a particle performing S.H.M. is
View Solution