Trajectory of a projectile is given by y=αx+βx2. Then find (α+β).
The correct Answer is:tan(θ)+g2u2cos2(θ)
To solve the problem, we need to find the sum of the coefficients α and β from the given projectile trajectory equation y=αx+βx2.
1. Identify the Given Equation:
The trajectory of the projectile is given by:
y=αx+βx2
2. Recall the General Equation of Projectile Motion:
The general equation for the trajectory of a projectile is:
y=xtanθ+gx22u2cos2θ
where:
- θ is the angle of projection,
- g is the acceleration due to gravity,
- u is the initial velocity.
3. Compare the Two Equations:
We will compare the coefficients of x and x2 in both equations:
- From the term αx, we can equate it to xtanθ:
α=tanθ
- From the term βx2, we can equate it to gx22u2cos2θ:
β=g2u2cos2θ
4. Find α+β:
Now, we need to find α+β:
α+β=tanθ+g2u2cos2θ
5. Final Answer:
Thus, the value of α+β is:
α+β=tanθ+g2u2cos2θ
The trajectory of the projectile is given by:
y=αx+βx2
The general equation for the trajectory of a projectile is:
y=xtanθ+gx22u2cos2θ
where:
- θ is the angle of projection,
- g is the acceleration due to gravity,
- u is the initial velocity.
We will compare the coefficients of x and x2 in both equations:
- From the term αx, we can equate it to xtanθ:
α=tanθ
- From the term βx2, we can equate it to gx22u2cos2θ:
β=g2u2cos2θ
Now, we need to find α+β:
α+β=tanθ+g2u2cos2θ
Thus, the value of α+β is:
α+β=tanθ+g2u2cos2θ
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Trajectory of particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion match the following with g=10ms−2.

View SolutionTrajectory of a particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion the following with g=10m/s2.
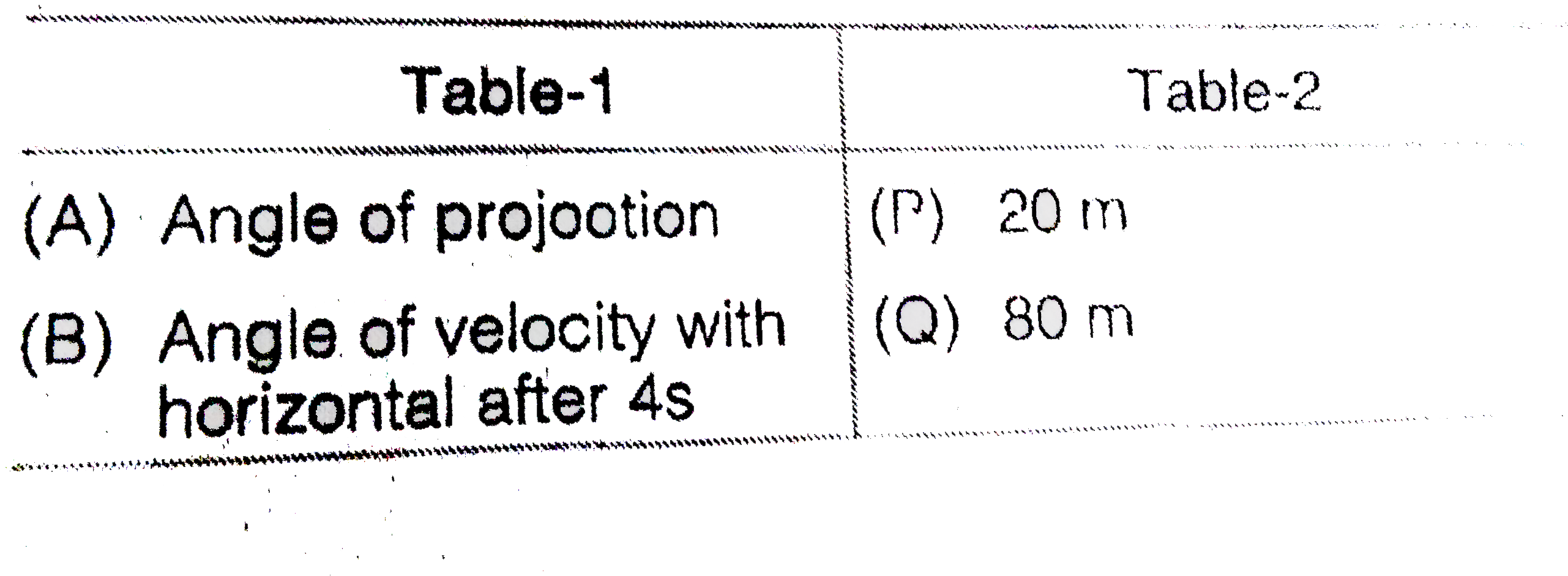
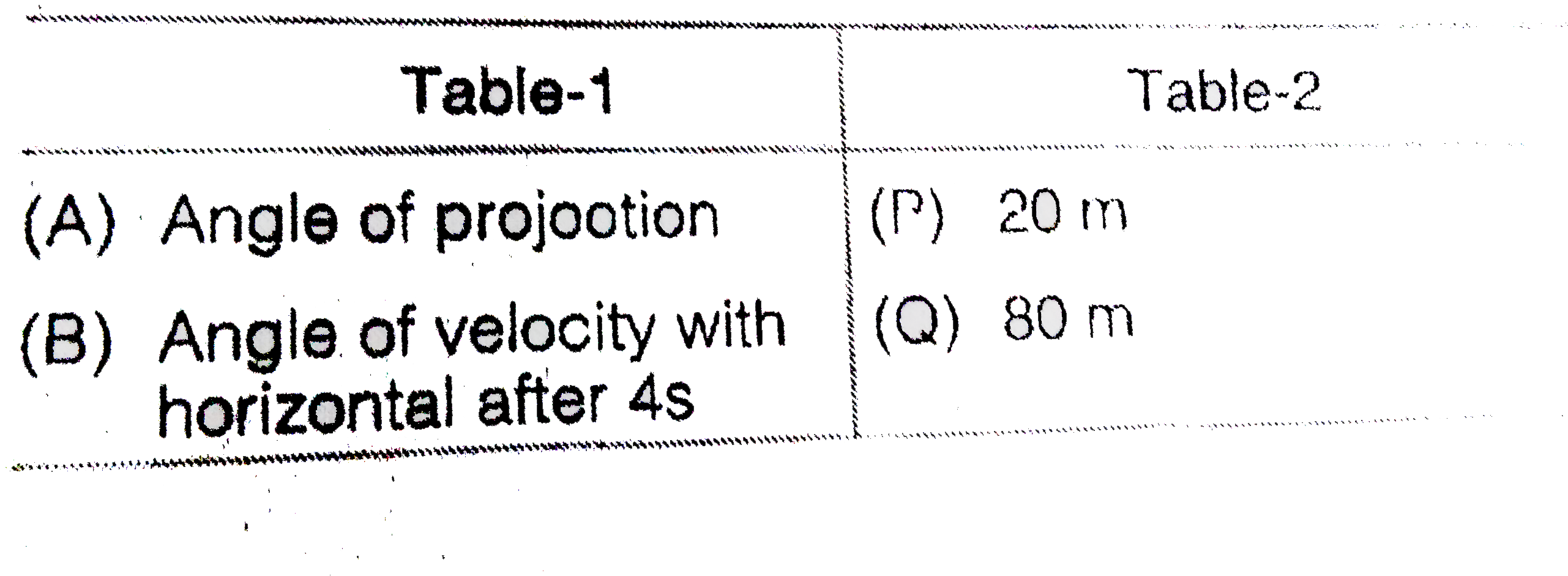
View Solution
Knowledge Check
An object is projected with a velocity of 10m/s at an angle 45∘ with horizontal. The equation of trajectory followed by the projectile is y=ax−βx2, the ratio α/β is
A5B10C15D20Energy due to position of a particle is given by, U=α√yy+β, where α and β are constants, y is distance. The dimensions of (α×β) are
A[M0LT0]B[M1/2L3/2T−2]C[M0L−7/2T0]D[ML7/2T−2]A particle is acted upon by a force given by F=−αx3−βx4 where α and β are positive constants. At the point x = 0, the particle is –
AIn stable equilibriumBIn unstable equilibriumCIn neutral equilibriumDNot in equilibrium
The equation of a trajectory of a projectile is y=8x−4x2. The maximum height of the projectile is ?
View SolutionTrajectory of particle in a projectile motion is given as: y=x−(x2/80) (x and y are in meters). Take g=10m/s2.

View Solution[" The equation of trajectory of a projectile is "],[y=ax-bx^(2)" where "x" and "y" axes are along "],[" horizontal and vertical directions "],[" respectively.The range of the projectile is "]
View SolutionThe displacement of a particle in a medium due to a wave travelling in the x−direction through the medium is given by y=Asin(αt−βx), where t= time, and α and β are constants:
View SolutionA particle is projected from the ground . Point of projection is taken as origin, horizontal direction as X-axis and verticle upward direction ass Y-axis. Equation of trajectory of the partcle is y=αx−βx2. Horizontal range of the projectile is
View Solution
