Let f(x)=ax3+bx+c. Then when f is odd, Solution in Telugu
c>0
c<0
c=0
c≥0
The correct Answer is:C
Step by step video, text & image solution for Let f(x) = ax^(3) + bx +c. Then when f is odd, by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNCTIONS BOOK - AAKASH SERIESCHAPTER - FUNCTIONS EXERCISE - EXERCISE -II
165 Videos
- ERRORS AND APPROXIMATIONSBOOK - AAKASH SERIESCHAPTER - ERRORS AND APPROXIMATIONSEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTION
15 Videos
- HEIGHTS AND DISTANCESBOOK - AAKASH SERIESCHAPTER - HEIGHTS AND DISTANCESEXERCISE - PRACTICE SHEET Exercise-I (Level-II) (Straight Objective Type Questions)
13 Videos
Similar Questions
If f(x)=logx,g(x)=x3 then f[g(a)]+f[g(b)]=
View SolutionFind the approximate value of log (2.01) give that log 2 = 0.6934
View SolutionThe angle of elevation of the top of a tower standing on a harzontal plane from the two points lying on a line passing through the foot of the tower at distances a and b respectively are complementary angles. If the line joining the two points sutends an angle θ at the top of the tower, then sinθ is
View SolutionLet a,b,c in R. If f(x)=ax^(2)+bx+c is such that a +b+c=3. If f(x)=ax^(2)+bx+c is such f(x+y)=f(x)+f(y)+xy AA x,y in R then sum_(n=1)^(10)f(n) is equal to
View SolutionLet a,b,c in R. If f(x)=ax^(2)+bx+c and a+b+c=3 and f(x+y)=f(x)+f(y)+xy then sum_(n=1)^(10)f(n) is
View SolutionLet f(x)=ax^(2)+bx+c, if f(-1) -1,f(3)<-4 and a!=0 then
View SolutionLet f(x)=ax^(2)+bx+c, where a,b,c,in R and a!=0, If f(2)=3f(1) and 3 is a roots of the equation f(x)=0, then the other roots of f(x)=0 is
View SolutionIf F(x)=Ax^(2)+Bx+C,and f(x) is integer when x is integer then
View SolutionLet f(x)=ax2+bx+csuch that f(1)=f(−1) and a, b, c, are in Arithmetic Progression.
f'(a), f'(b), f'(c) are
View SolutionLet f(x)=ax2+bx+csuch that f(1)=f(−1) and a, b, c, are in Arithmetic Progression.
f"(a), f"(b), f"(c) are
View SolutionLet f(X)=ax2+bx+c. Consider the following diagram
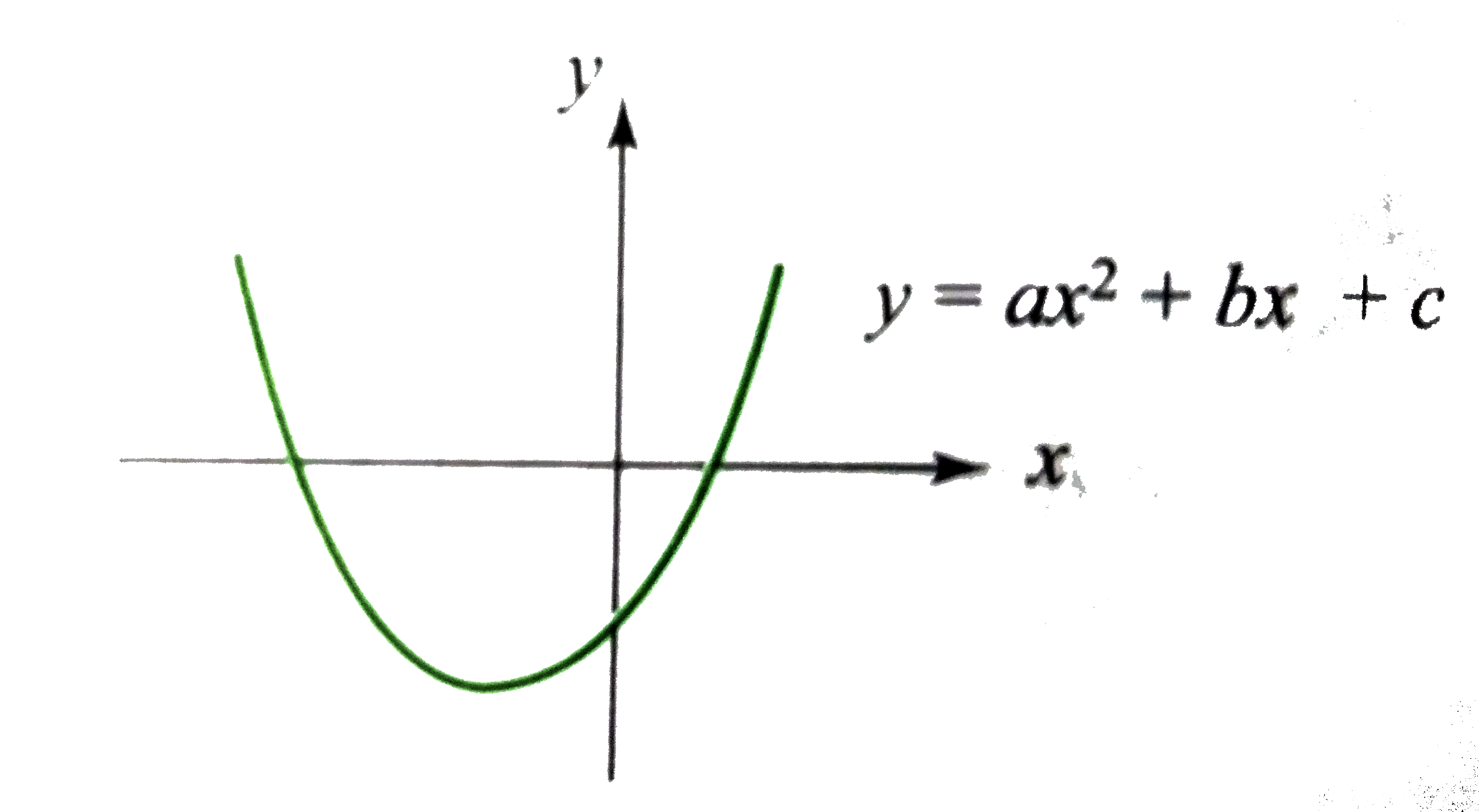 .
.
View SolutionLet f:[−3,3]→R defined by f(x)=[x2a]tanax+sexax. Then
If f(x) is an odd function, then
View SolutionIf f(x) =ax2+bx+c and f(1)=3 and f(-1)=3, then a+c equals
View SolutionLet f(x)=eaxsin(bx+c)and f''(x)=r2eaxsin(bx+θ),then-
View SolutionLet f(x)=ax2+bx+c,if a>0 then f(x) has minimum value at x=
View Solution
