Show that a bar magnet behaves as an equivalent current carrying solenoid.

Text Solution

Verified by Experts

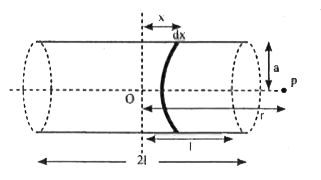
Let .a. be radius of solenoid of length 2l. To calculate magnetic field at a point on the a x is of a solenoid, consider a small element of thickness ‘dx. of solenoid at a distance .x. from .O..
Number of turns in this element =n.dx
If current .l. flows through element n dx the magnitude of magnetic field at ‘P. due to this element is
$d B = \frac{μ_{0}}{4 π} \frac{2 π (n d x) I a^{2}}{{[{(r - x)}^{2} + a^{2}]}^{1 / 2}}$
If point .P. is at large distance from .O. i.e., r >>x and r >> a then $[{(r - x)}^{2} + a^{2}] = r^{2}$
$d B = \frac{μ_{0}}{4 π} \frac{2 π (n d x) I a^{2}}{{(r^{2})}^{3 / 2}}$
$d B = \frac{μ_{0}}{4 π} \frac{2 π (n d x) I a^{2}}{r^{3}}$
The total magnetic field at .P. due to the current .I. in solenoid is
$B = \int_{- 1}^{1} d B = \int_{- 1}^{1} \frac{μ_{0}}{4 π} \frac{2 π n I a^{2} d x}{r^{3}}$
$B = \frac{μ_{0}}{4 π} \frac{2 π n I a^{2}}{r^{3}} \int_{- 1}^{1} d x$
$B = \frac{μ_{0}}{4 π} \frac{2 π n I a^{2}}{r^{3}} {[x]}_{- 1}^{1}$
$B = \frac{μ_{0}}{4 π} \frac{2 π n I a^{2}}{r^{3}} [l + l]$
$B = \frac{μ_{0}}{4 π} \frac{2 I n π a^{2} 2 l}{{(r)}^{3}}$
$B = \frac{μ_{0}}{4 π} \frac{2 I n A .2 l}{r^{3}} (∵ π a^{2} = A)$
$B = \frac{μ_{0}}{4 π} \frac{2 (n .2 l) I A}{r^{3}}$
$B = \frac{μ_{0}}{4 π} \frac{2 N I A}{r^{3}}$
$B = \frac{μ_{0}}{4 π} \frac{2 m}{r^{3}}$
This equation is similar to expression for magnetic field on the axis of a short bar magnet. Hence a solenoid carrying current behaves as a bar magnet.

Updated on:21/07/2023

What is a solenoid? Draw magnetic field lines due to a current carrying solenoid.
Aparabolic
Bcurved
Cstraight
Dcircular
Magnetic lines of force inside a current carrying solenoid are
APerpendicular to axis
BAlong the axis and are parallel to each other
CParallel inside the solenoid and circular at the ends
DCircular