एक समतल निर्देशांक अक्षों पर A, B,C पर अन्तःखण्ड abc बनाते हैं। यदि AABC का केन्द्रक, (3,2, 1) पर है, तब समतल का समीकरण है
x+2y+3z=9
2x−3y−6z=18
2x+3y+6z=18
2x+y+6z=18
The correct Answer is:C
Step by step video, text & image solution for एक समतल निर्देशांक अक्षों पर A, B,C पर अन्तःखण्ड abc बनाते हैं। यदि AABC का केन्द्रक, (3,2, 1) पर है, तब समतल का समीकरण है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - MULTIPLE CHOICE QUESTIONS (रेखा व समतल)31videos
त्रिविमीय निर्देशांक ज्यामिति
- BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - EXERCISE90videos
त्रिविमीय निर्देशांक ज्यामिति
- BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - MULTIPLE CHOICE QUESTIONS (रेखा)22videos
त्रिविमीय निर्देशांक ज्यामिति
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)5videos
त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकाये
- BOOK - ERRORLESS HINDICHAPTER - द्विपद प्रमेय तथा गणितीय आगमन EXERCISE - JEE Advanced (Matrix Math type questions)5videos
द्विपद प्रमेय तथा गणितीय आगमन
Similar Questions
बिन्दुओ (2,-3,1) तथा (3-4,5) को मिलाने वाली रेखा समतल 2x+y+z=7 को जिस बिन्दु पर काटती है, वह बिन्दु है
03:55View Solutionयदि l1,m1,n1 व l2,m2,n2 दो परस्पर लम्बवत् रेखाओं की दिक कोज्यायें हों, तो दोनों रेखाओं पर लम्ब रेखा की दिक कोज्यायें होंगी
02:03View Solutionबिन्दु (x1,y1,z1) की रेखा x−x2l=y−y2m=z−z2n से दुरी, जहाँ l,m,n रेखा की दिक् कोज्यायें हैं, है
02:15View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
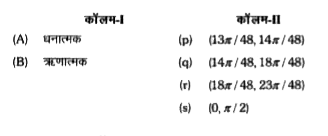 02:37View Solution
02:37View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
 02:14View Solution
02:14View Solutionबिन्दुओ (4,-1,2) और (-3,2,3) को मिलाने वाली रेखा एक समतल को बिंदु (-10,5,4) पर लंबवत मिलती है समतल का समीकरण ज्ञात कीजिये
01:44View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
03:50View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
03:15View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
04:05View Solutionउस समतल का समीकरण ज्ञात कीजिए, जो अक्षों से समान अन्तःखण्ड काटता है तथा बिंदु (2, 3, 4) से होकर जाता है |
03:18View Solutionउस समतल का समीकरण ज्ञात कीजिए जो X, Y और Z-अक्षों पर क्रमशः 1, 2 और 3 अन्तःखण्ड काटता है |
03:38View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
04:32View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
06:39View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
47:25View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
03:43View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
02:24View Solution

