उस समतल का समीकरण, जो समतलों x+2y+3z-5-0, x+2y+3z-7=0 के समतुल्रय है और उनसे सामान दुरी पर है
x+2y+3z−6=0
x+2y+3z−1=0
`x+2y+3z-8=0`
x+2y+3z−3=0
The correct Answer is:A
Step by step video, text & image solution for उस समतल का समीकरण, जो समतलों x+2y+3z-5-0, x+2y+3z-7=0 के समतुल्रय है और उनसे सामान दुरी पर है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (MORE THAN ONE CORRECT ANSWERS)
10 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (REASONIG TYPE QUESTIONS)
10 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - MULTIPLE CHOICE QUESTIONS (रेखा व समतल)
31 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
- द्विपद प्रमेय तथा गणितीय आगमन BOOK - ERRORLESS HINDICHAPTER - द्विपद प्रमेय तथा गणितीय आगमन EXERCISE - JEE Advanced (Matrix Math type questions)
5 Videos
Similar Questions
एक रेखा l जो मूलबिंदु से गुजरती है रेखाओं
l1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk,−∞<t<∞
l2:(3+2s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<s<∞
पर लम्बवत है। तब l2 पर स्थित बिंदु (बिंदुओं) के निर्देशांक जो रेखाओं l तथा l1 के प्रतिच्छेद बिंदु से √17 की दूरी पर है निम्न है: (i) (73,73,53) (ii) (−1,−1,0)
(iii) (1,1,1) (iv) (79,79,89)
View Solutionकथन-1: रेखा x1=y−12=z−23 में बिन्दु B(1, 6, 3) का दर्पण प्रतिबिम्ब (mirror image) बिन्दु A(1, 0, 7) है:
कथन-2: रेखा x1=y−12=z−23 बिंदुओं A(1,0,7) तथा B(1,6,3) को मिलाने वाले रेखाखण्ड का समद्विभाजन करती है।
View Solutionबिन्दुओ (2,-3,1) तथा (3-4,5) को मिलाने वाली रेखा समतल 2x+y+z=7 को जिस बिन्दु पर काटती है, वह बिन्दु है
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
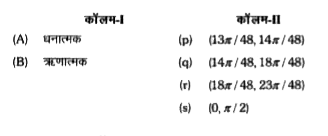
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये

View SolutionEquation of the plane parallel to the planes
x+2y+3z−5=0, x+2y+3z−7=0 and equidistant from them is
View Solutionबिन्दु `(1,0,0)` से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओ x=−3 तथा x=5 से समान दूरी पर है ।
View Solutionउस समतल का समीकरण ज्ञात कीजिए जो X, Y और Z-अक्षों पर क्रमशः 1, 2 और 3 अन्तःखण्ड काटता है |
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionउस समतल का समीकरण ज्ञात कीजिए जो x,y और z-अक्षो पर क्रमश: 2,3 और 4 अंत: खंड काटता है।
View Solutionयदि समीकरण निकाय x+y+z=5,x+2y+3z=9,x+3y+αz=β के अंसख्य हल है, तो β−α बराबर है
View Solutionउस सरल रेखा का समीकरण जो बिन्दु (1,-2) से गुजरती है तथा रेखा 3x-5y+7=0 के लम्बवत है, है
View Solutionउस सरल रेखा का समीकरण जो रेखाओं 3x-y+ 2 = 0 तथा 5x-2y+ 7 = 0 के प्रतिच्छेद बिन्दु से गुजरती है तथा जिसकी प्रवणता अनन्त है, होगा
View SolutionThe system of equations x-2y+3z=5, 2x-2y+z=0, -x+2y-3z=6 has
View Solution
