माना कि रेखाएं निम्न हैं L1:x+13=y+21=z+12:L2x−21=y+22=z−33
बिन्दु (-1, -2, -1) से गुजरने वाले समतल की बिन्दु (1, 1, 1) से दूरी, जिसका अभिलम्ब रेखाओं L1 तथा L2 दोनों के लम्बवत् है,
2√75
7√75
13√75
`(23)/(sqrt(75))`
The correct Answer is:C
Topper's Solved these Questions
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-III)
3 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-IV)
3 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (COMPREHENSION TYPE QUESTIONS) (PASSAGE-I)
3 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
- द्विपद प्रमेय तथा गणितीय आगमन BOOK - ERRORLESS HINDICHAPTER - द्विपद प्रमेय तथा गणितीय आगमन EXERCISE - JEE Advanced (Matrix Math type questions)
5 Videos
Similar Questions
एक प्रकाश की किरण रेखा L = 0 के अनुदिश आती है और B पर समतल P=0 के अनुदिश रखे समतल दर्पण से टकराती है बिन्दु A(2,1,6) रेखा L=0 पर स्थित है जिसका प्रतिबिम्ब P=0 के सापेक्ष A है, यह दिया जाता है कि L=0,x−23=y−14=z−65 है तथा P=0,x+y−2z=3 है।
A' के निर्देशांक हैं
View Solutionमाना तीन समतल `2x + py+62 = 8,x+2y+qz = 5` तथा `x+y+3z=4` है।
तीन समतल एक बिन्दु पर प्रतिच्छेद करते है यदि
View Solutionमाना कि a,b,c ऐसी तीन वास्तविक संख्यायों हैं जो
[abc]⎡⎢⎣197827737⎤⎥⎦=[000] को संतुष्ट करती हैं।
यदि समीकरण E के संदर्भ में बिंदु P(a,b,c) समतल 2x+y+z=1 पर स्थित है तो 7a+b+c का मान है
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
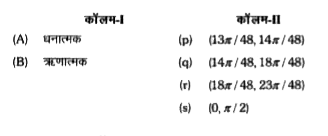
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये

View SolutionConsider the line L1:x+13=y+21=z+12,L2:x−21=y+22=z−33 The shortest distance between L1andL2 is
View SolutionConsider the line L1:x+13=y+21=z+12,L2:x−21=y+22=z−33 The shortest distance between L1andL2 is
View SolutionRead the following passage and answer the questions. Consider the lines
L1:x+13=y+21=z+12
L2:x−21=y+22=z−33
Q. The shortest distance between L1andL2 is
View Solution`L_(1):(x+1)/(-3)=(y-3)/(2)=(z+2)/(1),L_(2):(x)/(1)=(y-7)/(-3)=(z+7)/(2)`
The lines `L_(1)` and `L_(2)` are -
View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
The lines L1 and L2 intersect at the point
View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
Equation of plane containinng L1 and L2 is -
View SolutionThe shortest distance between lines
L1:x+13=y+21=z+12,
L2:x−21=y+22=z−33 is
View Solutionएक समतल जो बिन्दु (1,−1,−1) से होकर जाता है तथा जिसका अभिलम्ब दोनों रेखाओं x−11=y+2−2=z−43 तथा x−22=y+1−1=z+7−1 पर लम्ब है, की बिन्दु (1,3,−7) से दुरी है
View Solutionमाना कि रेखाएं निम्न हैं L1:x+13=y+21=z+12:L2x−21=y+22=z−33
L1 तथा L2 के बीच की न्यूनतम दूरी है
View Solutionरेखाओं L1:x+13=y+21=z+12,L2:x−21=y+22=z−33 पर विचार कीजिए।
दोनों रेखाओं L1 व L2 के लम्बवत इकाई सदिश है
View Solutionरेखाओं `L_(1):(x+1)/3=(y+2)/1=(z+1)/2, L_(2): (x-2)/1=(y+2)/2=(z-3)/3` पर विचार कीजिए।
`L_(1)` तथा `L_(2)` के बीच की न्यूनतम दूरी है
View Solution
