In ΔABC, AD and BE are altitudes. If BC=8, AC=12 and AD=6, find ar (ABC) and BE. Solution in Gujrati
The correct Answer is:ar (ABC)=24 ,BE=4
Step by step video, text & image solution for In DeltaABC, AD and BE are altitudes. If BC=8, AC=12 and AD=6, find ar (ABC) and BE. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - QUESTION PAPER 2: FOR THE SECOND TESTEXERCISE - SECTION C (Solve the following :)4videos
QUESTION PAPER 2: FOR THE SECOND TEST
- BOOK - KUMAR PRAKASHANCHAPTER - QUESTION PAPER 2: FOR THE SECOND TESTEXERCISE - SECTION D (Solve the following :)5videos
QUESTION PAPER 2: FOR THE SECOND TEST
- BOOK - KUMAR PRAKASHANCHAPTER - QUESTION PAPER 2: FOR THE SECOND TESTEXERCISE - SECTION D (Solve the following :)5videos
QUESTION PAPER 2: FOR THE SECOND TEST
- BOOK - KUMAR PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - MULTIPLE CHOICE QUESTION(MCQs)15videos
QUADRILATERALS
- BOOK - KUMAR PRAKASHANCHAPTER - QUESTION PAPER 3 : FOR THE ANNUAL EXAMINATION EXERCISE - SECTION -D5videos
QUESTION PAPER 3 : FOR THE ANNUAL EXAMINATION
Similar Questions
In the given figure, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
 04:07View Solution
04:07View SolutionLocate √3 on number line
02:34View SolutionLocate √3 on number line
07:14View SolutionThe ratio of four angles in order of a quadrilateral is 2:4:5: 4. Then, the measure of the smallest angle of the quadrilateral is ………..
03:29View SolutionProve that the angles opposite to equal sides of an isosceles triangle are equal.
03:00View SolutionIn Delta ABC,AD perp BC,AD=6,BC=8 then find distance between mid-points of BD and AC
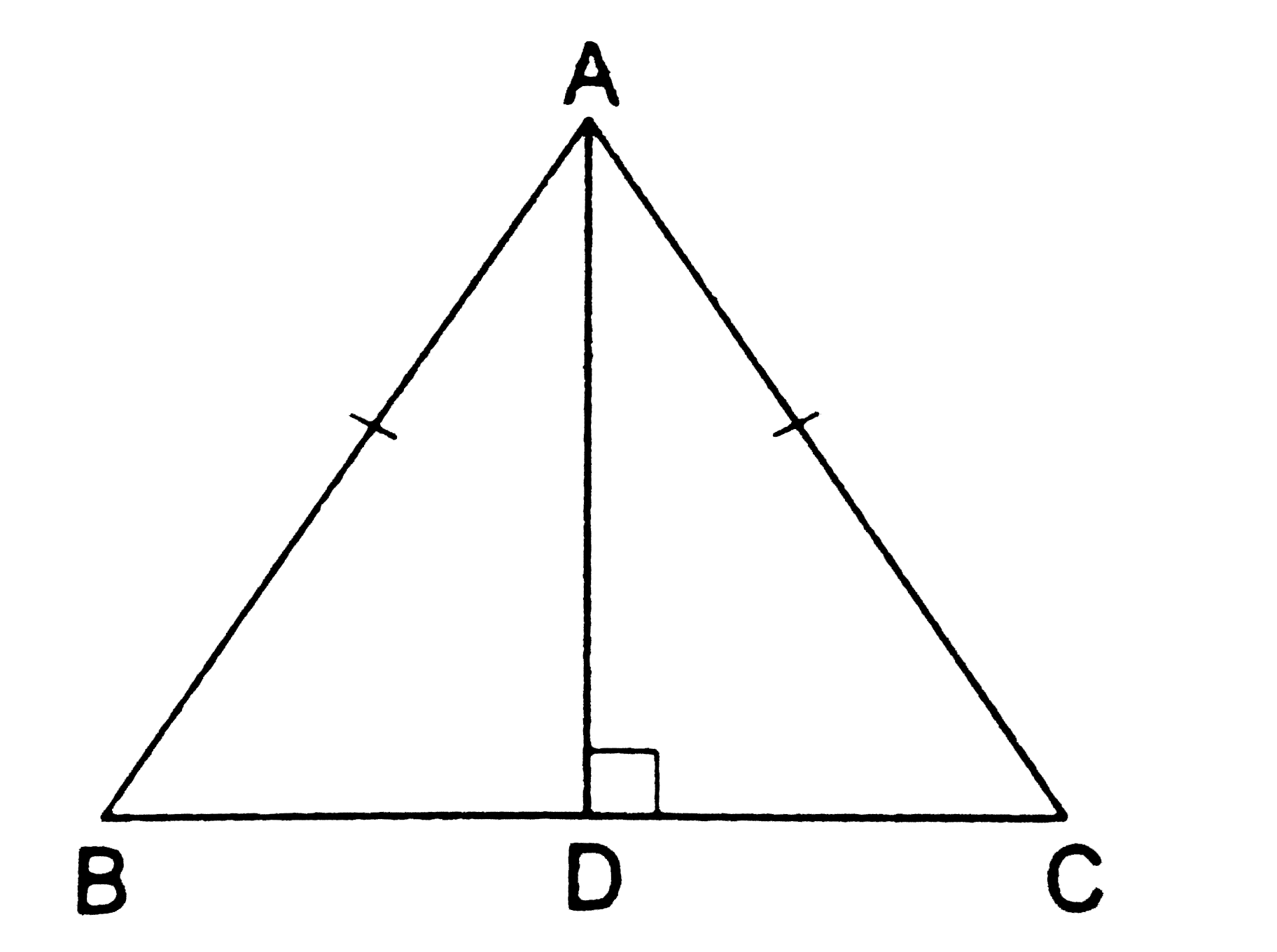
05:33View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
 06:11View Solution
06:11View Solution(a) ΔABC में , AB=5 सेमी , BC = 13 सेमी तथा AC = 12 सेमी है । यदि BC का मध्य बिंदु D है , तो माध्यिका AD कि माप ज्ञात कीजिए ।
(b) निम्न चित्र में ,ΔABC की माध्यिक AD=6 सेमी है । यदि आधार BC = 8 सेमी हो तो का AB2+AC2 मान ज्ञात कीजिए ।03:20View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
 05:29View Solution
05:29View Solution△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
03:04View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
01:35View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
02:43View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
07:19View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
02:57View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
 View Solution
View Solution

