In ΔABC, 'O' is the orthocentre, M is midpoint of BC and ∠BAC=30∘. The segment OM is produced to the point T such that OM = MT. Prove that AT=2BC.Solution in Telugu
Step by step video & image solution for In DeltaABC, 'O' is the orthocentre, M is midpoint of BC and angleBAC = 30^(@). The segment OM is produced to the point T such that OM = MT. Prove that AT=2BC. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DOT PRODUCT OF TWO VECTORSBOOK - AAKASH SERIESCHAPTER - DOT PRODUCT OF TWO VECTORSEXERCISE - EXERCISE-2.1 (VERY SHORT ANSWER QUESTIONS)
6 Videos
- DOT PRODUCT OF TWO VECTORSBOOK - AAKASH SERIESCHAPTER - DOT PRODUCT OF TWO VECTORSEXERCISE - EXERCISE-2.1 (SHORT ANSWER QUESTIONS)
18 Videos
- DOT PRODUCT OF TWO VECTORSBOOK - AAKASH SERIESCHAPTER - DOT PRODUCT OF TWO VECTORSEXERCISE - PRACTICE EXERCISE
57 Videos
- DIRECTION COSINES AND RATIOSBOOK - AAKASH SERIESCHAPTER - DIRECTION COSINES AND RATIOSEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
8 Videos
- ERRORS AND APPROXIMATIONSBOOK - AAKASH SERIESCHAPTER - ERRORS AND APPROXIMATIONSEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTION
15 Videos
Similar Questions
If bara = 6bari+2barj+3bark and barb = 2bari - 9barj+6bark , " then find " bara.barb " and the angle between " bara and barb .
View SolutionIf ¯a=2¯i+2¯j−3¯k,¯b=3¯i−¯j+3¯k, then find the angle between 2¯a+¯band¯a+2¯b.
View SolutionIf ¯¯μ=¯a−¯b,¯v=¯a+¯band|¯a|=∣∣¯b∣∣, then ¯¯μ.¯v is
View SolutionIf the line joining the points (2,k,5), (0,1,6) is parallel to the line joining the points (3,-1,2), (-1,2,4) then find k,
View SolutionFind the approximate value of log (2.01) give that log 2 = 0.6934
View SolutionIn triangle ABC,∠A=300,H is the orthocenter and D is the midpoint of BC. Segment HD is produced to T such that HD=DT The length AT is equal to
(a). 2BC
(b). 3BC
(c). 42BC
(d). none of these
View SolutionIn Delta ABC,|_(BAC)=30^(@) and H is the orthocentre,M is the mid point of BC.HM is produced to thepoint T such that HM=MT Then |AT|=lambda|BC| where lambda is
View SolutionIf two points M and N on the hyperbola (x^(2))/(5)-(y^(2))/(9)=45 (whose centre is O),be such that OM is perpendicular to ON then the value of (OM^(2)+ON^(2))/(OM^(2)+ON^(2)) is equal to 3 )
View SolutionΔABC में, ∠BAC=90∘ तथा AB=12BC है, तब ∠ACB है।
View SolutionP is any point on the circumference of the circumcircle of ΔABC. H is the orthocentre, M is the midpoint of PH and D is the midpoint of BC. Then
View SolutionIn triangle ABC,∠A=300,H is the orthocenter and D is the midpoint of BC. Segment HD is produced to T such that HD=DT. The length AT is equal to a. 2BC b. 3BC c. 42BC d. none of these
View SolutionIn a circle with centre 'O' . ¯¯¯¯¯¯AB is a chord and 'M' is its midpoint . Now prove that ∠(OM) is perpendicular to AB
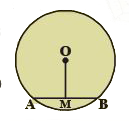
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on ¯¯¯¯¯¯AB and ¯¯¯¯¯¯ON is perpendicular on ¯¯¯¯¯¯CD. Then prove that OM = ON.

View SolutionIn a circle with centre 'O' . bar(AB) is a chord and 'M' is its midpoint . Now prove that bar(OM) is perpendicular to AB
View SolutionIn the figure, O is the centre of the circle and AB = CD. OM is perpendicular on bar(AB) and bar(ON) is perpendicular on bar(CD) . Then prove that OM = ON.
View Solution
