Find the orthocentre of the triangle formed by x+y+10=0,x−y−2=0,2x+y−7=0.Solution in Telugu
The correct Answer is:(-4,-6)
Step by step video, text & image solution for Find the orthocentre of the triangle formed by x+y+10=0,x-y-2=0, 2x+y-7=0. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINESBOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - ADDITIONAL SOLVED EXAMPLES
12 Videos
- STRAIGHT LINESBOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 3.1 (VERY SHORT ANSWER QUESTIONS)
11 Videos
- STRAIGHT LINESBOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II (ADVANCED) PRACTICE SHEET (ADDVANCED)) (Comprehension Type Questions)
6 Videos
- REVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - REVISION EXERCISEEXERCISE - PROPERTIES OF TRIANGLES
57 Videos
- TANGENT AND NORMAL BOOK - AAKASH SERIESCHAPTER - TANGENT AND NORMAL EXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
48 Videos
Similar Questions
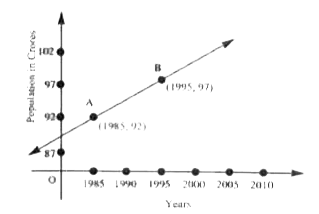
Consider the following population and year graph, find the slope of the line AB and using it, find what will be the population in the year 2010?
View SolutionFind the slope of the line whose inclination is
30∘
View SolutionLet A(0,0), B (5,0), C (5,3) and D(0,3) be the vertice of rectiangle ABCD , If P is a variable point lying inside the rectangle ABCD and d (P,L) denotes perpendicular distance of point P from line L
If ≤min{d(P,BC),d(P,CD),d(P,AD)}, then area of the region in which P lies is (in sq. units
View SolutionIn a triangle ABC, if A,B, C are in A.P and b:c =√3:√2, then
View SolutionFind the equations of tangent and normal to the curve
(xa)4+(yb)4=2 at (a,b)
View SolutionThe orthocentre of the triangle formed by the lines x-2y+9= 0, x + y -9 =0, 2x -y-9=0is
View SolutionThe orthocentre of the triangle formed by the pair of lines 2x2−xy−y2+x+2y−1=0 and the line x+y+1=0, is
View SolutionThe orthocentre of triangle formed by lines x+y−1=0,2x+y−1=0andy=0 is (h, k), then 1k2=
View SolutionFind the orthocentre of the triangle whose sides are 7x+y−10=0,x−2y+5=0,x+y+2=0
View SolutionFind the orthocentre of the triangle whose sides are 7x+y−10=0,x−2y+5=0,x+y+2=0
View SolutionThe orthocentre of the triangle formed by the lines x−2y+9=0,x+y−9=0,2x−y−9=0 is
View SolutionThe orthocentre of triangle formed by lines x+y−1=0,2x+y−1=0andy=0 is (h, k), then 1k2=
View SolutionOrthocentre of the triangle formed by the lines x+y+1=0 and 2x2+y2+x+2y−1=0 is
View SolutionOrthocentre of triangle formed by the lines x2−xy−x+y=0and2x−y+4=0 is
View SolutionFind the circumcentre of the triangle formed by the lines x+y=0,2x+y+5=0 and x−y=2
View Solution